Ackermannlenkung

Einfache Sprache

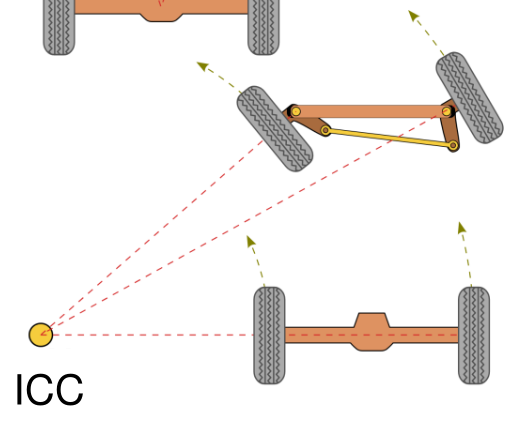
Die Ackermannlenkung beschreibt die Erweiterung des Differentialantriebs mit mehr Räder (Rad) die gedreht werden können. So kann trotzdem ein Momentanpol $\text{ICC}$ gefunden werden.

Theorie mit einem drehbaren Rad

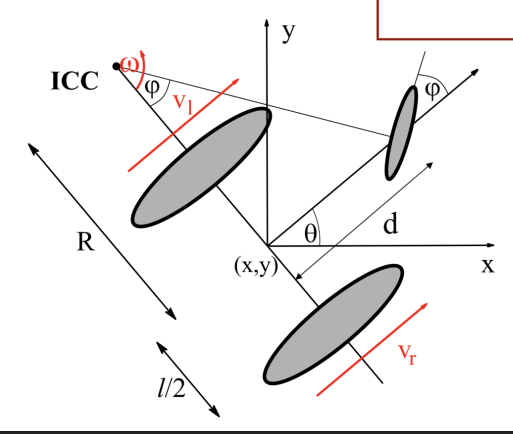
Die Formeln für $v_r$, $v_l$, $\text{ICC}$ und $\omega$ ergeben sich Analog zum Differentialsantrieb. Für den Wenderadius $R$ ergibt sich jedoch zwei Gleichungen. (1) Es muss zum einen die Gleichung aus dem Differentialsantrieb erfüllt sein, die besagt, dass sich $R$ aus den einzelnen Geschwindigkeiten der Räder ableitet. (2) Andererseits muss das drehbare Rad so gedreht sein, dass die Tangente des Rades das, aus der ersten Gleichung resultierende, Momentanpol schneidet. Also