Differentialsantrieb

Einfache Sprache

Beim Differentialsantrieb liegen zwei angetriebene Räder (Rad) auf der selben Achse und werden unabhängig voneinander angetrieben. Damit kann vor, zurück und im Kreis gefahren werden. Hier sind die internen Bewegungen rot und die externen Bewegungen blau.

Theorie

Gegeben seien zwei Räder (Rad) auf einer Achse, die getrennt voneinander angetrieben werden und $l$ voneinander entfernt sind. Die Geschwindigkeit der Räder $v_l$ und $v_r$ berechnet sich durch Winkel $w_i$ mal Radius des Rads $r$. Also $v_i = w_ir_i$.

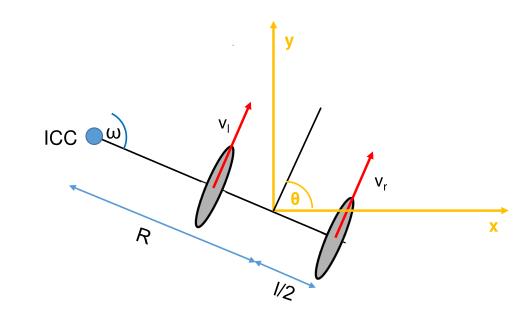Wir wollen nun, das sich das Gefährt um einen festen Punkt $\text{ICC}$ fährt. Hier ist der $\text{ICC}$ ein Momentanpol. Sich also entlang der Tangente eines Kreises mit dem Mittelpunkt $\text{ICC}$ bewegt. Das Gefährt ist insgesamt $R$ von $\text{ICC}$ entfernt. Die beiden Räder sind $l$ voneinander entfernt. Wir nehmen jetzt an das der $\text{ICC}$ sich links in Fahrtrichtung befindet. Dann müssen bei einer Fahrt um den Mittelpunkt von $\omega$ Grad die Räder die folgende Geschwindigkeit haben

Nun stellt man die Gleichungen nach $R$ um, setzt sie gleich und vereinfacht um

zu erhalten. Die Formel beschreibt wie der Wendewinkel von den Geschwindigkeiten und der Distanz zwischen den Rädern abhängt. Ersetzen wir $\omega$ nun in den Formeln für $v_r$ und $v_l$ erhalten wir Wenderadius als

Daraus ergibt sich die Gesamtgeschwindigkeit des Gefährts als

Um die Position des Momentanpol $\text{ICC}$ zu ermitteln brauchen wir ein “Welt-Koordinatensystem”. Das ist hier in Gelb gegeben. Wir gehen davon aus, dass das Gefährt weis wo es sich in ihm befindet. Also $x$ und $y$ sind bekannt. Sei $\theta$ nun der Winkel zwischen $v$ und der $x$-Achse. $\theta$ ist also die Drehung des Gefährts im Raum. Dann der Momentanpol wie folgt gegeben:

Vorwärts-Kinematik

Für die Vorwärtsbewegung ergibt sich nun folgendes Bild. 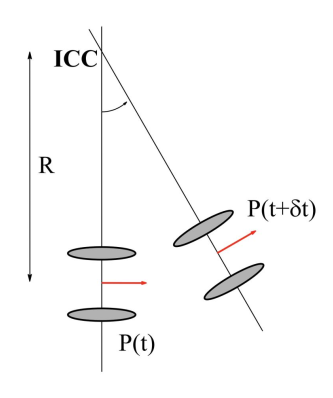Sei $\mathfrak P(t)$ die Position des Gefährts zum Zeitpunkt $t$. Die Position ist dabei eine Vektor bestehend aus der Position im Raum $(x,y)$ und der Ausrichtung des Gefährts von der $x$-Achse $\theta$.
Um $\mathfrak P(t)$ um den $\text{ICC}$ zu drehen benutzen wird die 2D-Drehmatrix

Um die für die Drehung brauchen wir dann noch den $R$ Vektor. Der ergibt sich in dem wir den Vektor zum Momentanpol $\text{ICC}$ vom Positionssvektor abziehen. $\theta$, die Drehung um Raum, verändert sich nur in dem Sinne, das der Drehungswinkel $\omega$ multipliziert mit dem Zeit $\delta t$ auf $\theta$ addiert wird um die neue Drehung im Raum zu erhalten. Daraus ergibt sich bei gegebenen Momentanpol $\text{ICC}$ und Zeitfenster $\delta t$ folgende Gleichung für die neue Position $\mathfrak p'$ als