Algorithmus von Boruvka und Sollin
Zusammenfassung
Ein Greedy-Algorithmus um Minimalen Spannbaume zu berechnen. Von einem zufälligen Startknoten ausgehend wird iterativ die kleinste Kante gewählt
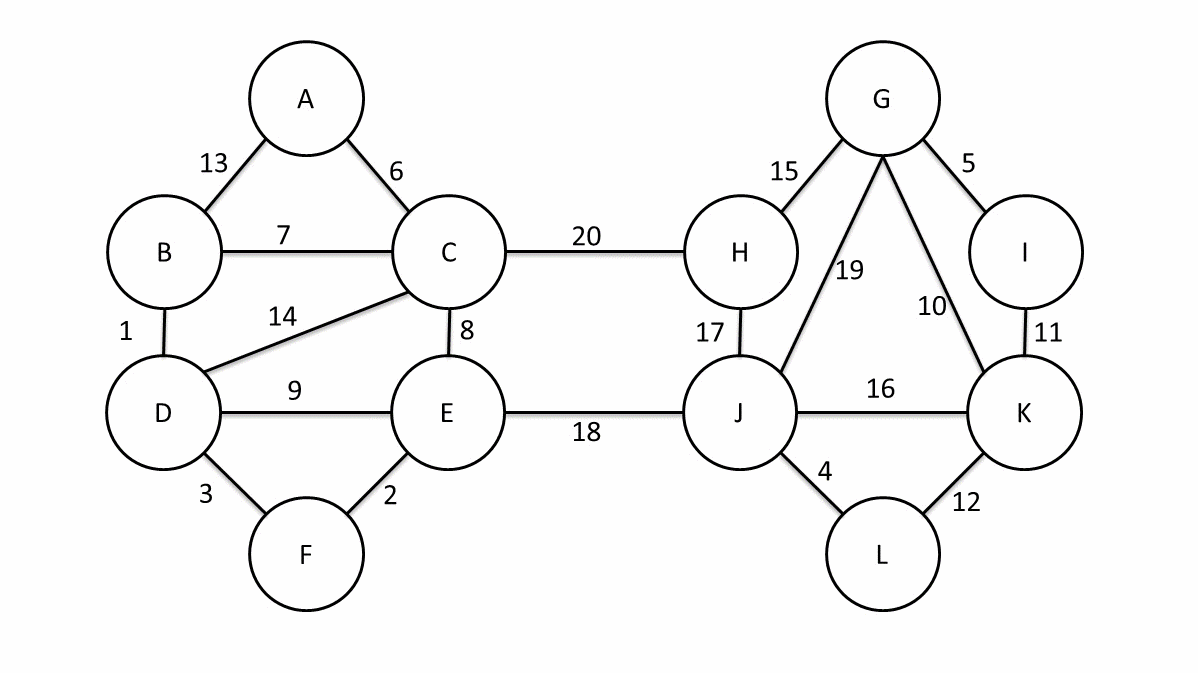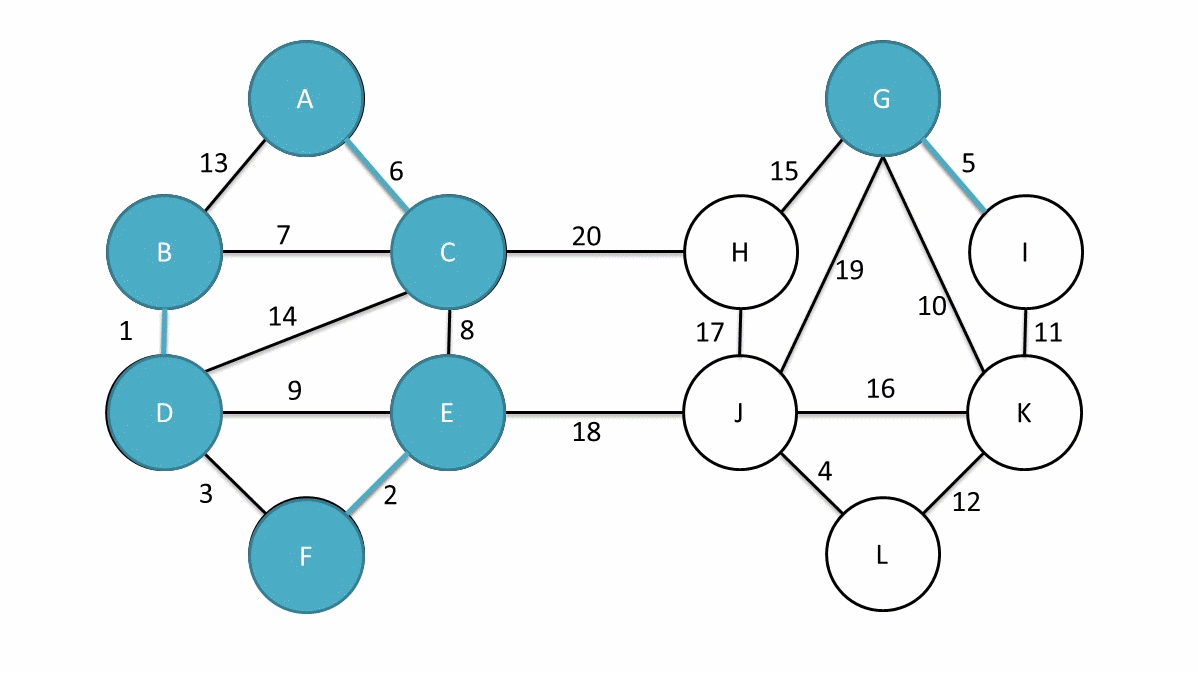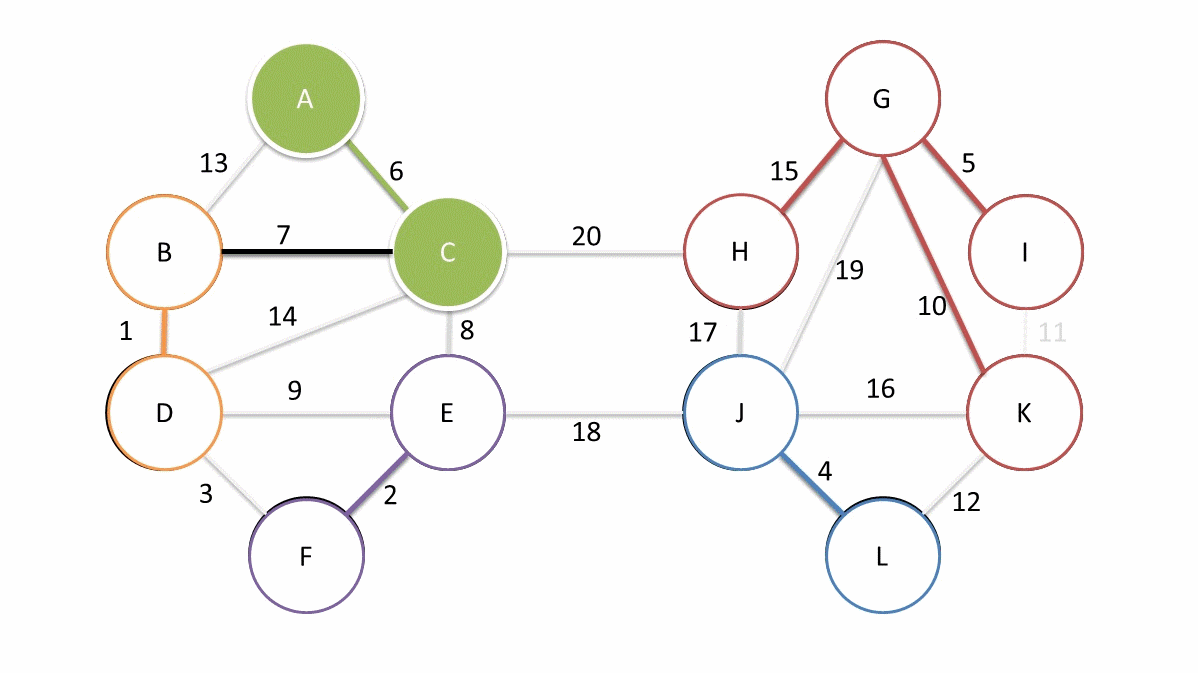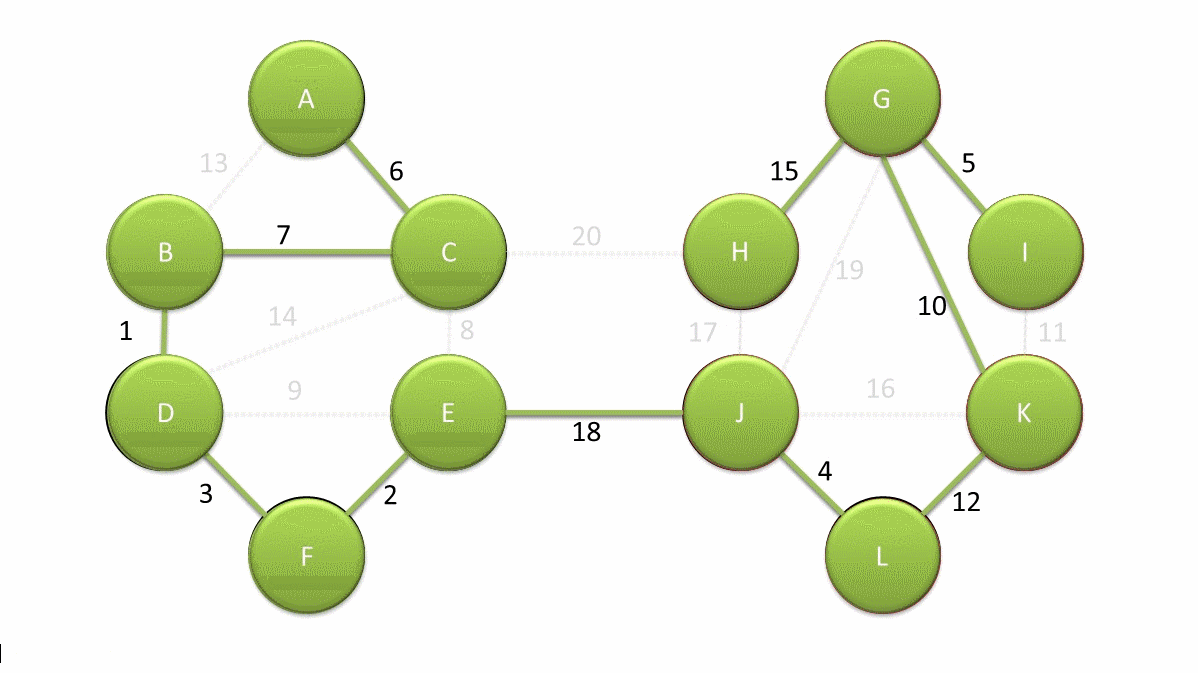
Idee Algorithmus von Boruvka und Sollin
Zu beginn werden $|V|$ Zusammenhangskomponente erstellt, welche jeweils eine Knoten beinhalten. In jeder Runde wird die leichteste ausgehende Kante jeder Zusammenhangskomponente ausgewählt und die, an dieser Kante beteiligten, Komponenten werden zu einer Komponenten über diese Kante verschmelzt. Der MST besteht genau aus diesen Kanten.
Algoritmus
1def boruvka_sollin(G, w):
2 V, E = G
3 n = len(V)
4 ET = set() # Initialize empty set for edges of MST
5 C = [{i} for i in range(n)] # Initial components (each vertex is its own component)
6
7 while len(C) != 1:
8 # Initialize min edge tracking for each component
9 min_edge = [float('inf')] * len(C)
10 shortest = [None] * len(C)
11
12 # Find cheapest outgoing edge for each component
13 for u, v in E:
14 # Find components containing u and v
15 i = next(idx for idx, S in enumerate(C) if u in S)
16 j = next(idx for idx, S in enumerate(C) if v in S)
17
18 if i != j: # Only consider edges between different components
19 weight = w[(u, v)]
20 # Update min edge for component i
21 if weight < min_edge[i]:
22 min_edge[i] = weight
23 shortest[i] = (u, v)
24 # Update min edge for component j
25 if weight < min_edge[j]:
26 min_edge[j] = weight
27 shortest[j] = (u, v)
28
29 # Add all found shortest edges to ET (avoid duplicates)
30 for edge in shortest:
31 if edge is not None:
32 ET.add(edge)
33
34 # Recompute components after adding new edges
35 # Build adjacency list for current forest
36 adj = {v: [] for v in range(n)}
37 for u, v in ET:
38 adj[u].append(v)
39 adj[v].append(u)
40
41 # Find connected components using DFS
42 visited = [False] * n
43 new_C = []
44 for v in range(n):
45 if not visited[v]:
46 stack = [v]
47 component = set()
48 while stack:
49 node = stack.pop()
50 if not visited[node]:
51 visited[node] = True
52 component.add(node)
53 for neighbor in adj[node]:
54 if not visited[neighbor]:
55 stack.append(neighbor)
56 new_C.append(component)
57 C = new_C
58
59 return (V, ET)
Die sequenzielle Laufzeit beträgt $\mathcal O(|E|\log|V|)$, da jede Runde $\mathcal O(|E|)$ benötigt und sich die Anzahl der verbleibenden Komponenten min. halbiert.