Algorithmus von Dijkstra

Einfache Sprache

Der Algorithmus von Dijkstra ist ein Greedy-Algorithmus der das Kürzeste Wegeproblem löst. Der Algorithmus verfolgt dabei immer diejenige Kanten, welchen den kürzesten Streckenabschnitt vom Startknoten aus versprechen.

Idee Algorithmus von Dijkstra

Verwende zwei disjunkte Mengen $P,Q$ mit $V=P\cup Q$ wobei Knoten $j\in P$ permanent mit $u_j$ und Knoten $j\in Q$ vorläufig mit $v_j \geq u_j$ gelabelt sind. Nutzt die Vervollständigte Entfernungsmatrix $A$. Voraussetzung damit Dijkstra funktioniert ist wir nur positive Kantenwerte haben.

Algorithmus

 1def dijkstra(G, A):
 2    V, E = G
 3    n = len(V)
 4    P = {0}  # Visited nodes (starting with source node 0)
 5    Q = set(range(1, n))  # Unvisited nodes
 6    distances = [float('inf')] * n  # Using float('inf') instead of sys.maxsize
 7    distances[0] = 0  # Distance from source to itself
 8    # Initialize distances from source
 9    for j in range(1, n):
10        distances[j] = A[0][j]
11    while len(P) != n:
12        # Find unvisited node with smallest distance
13        k = min(Q, key=lambda x: distances[x]) 
14        P.add(k)
15        Q.remove(k)
16        # Update distances to neighbors
17        for j in Q:
18            if A[k][j] != float('inf'):
19                distances[j] = min(distances[j], distances[k] + A[k][j])
20    return distances

Laufzeit

Die Laufzeit von Dijkstra ist $\mathcal O(|V|^2)$. Mit Fibonacci-Heaps ist sie $\mathcal O(|E| + |V|\log|V|)$.

Example

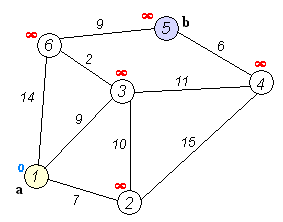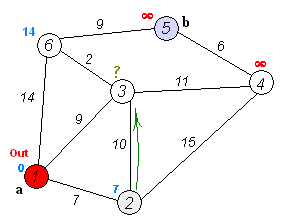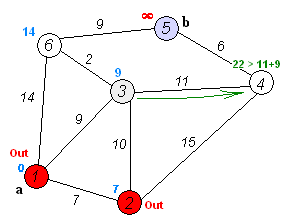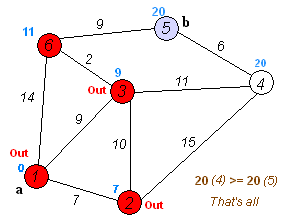
Gegeben sei folgender Graph: Der Algorithmus von Dijkstra produziert folgende Tabelle: D.h. wir erhalten $u_1 = 0, u_2 = −1, u_3 = 1, u_4 = 2 \text{ und } u_5 = 2$. (Also z.B. ist die Länge des kürzesten Weges zu $u_4$ gleich $2$)