Algorithmus von Prim
Zusammenfassung
Ein Greedy-Algorithmus um Minimalen Spannbaume zu berechnen. Von einem zufälligen Startknoten ausgehend wird iterativ die kleinste Kante gewählt.
Idee Algorithmus von Kruskal
Zuerst wird ein zufälliger Startknoten gewählt. Dieser bildet dann die Zusammenhang > Zusammenhangskomponente. Ausgehend von dieser Zusammenhangskomponente wird die kleinste ausgehende Kante (also eine, die nicht innerhalb der Komponente verläuft) gewählt. Der Knoten zu dem die Kante führt wird dann der Zusammenhangskomponente angefügt. Das wird solange wiederholt bis alle Knoten in der Zusammenhangskomponente sind.
Algorithmus
1def prim_jarnik_naive(G, w):
2 V, E = G
3 n = len(V)
4 U = {0} # Using 0-based index (1 becomes 0)
5 ET = set()
6 for _ in range(n-1):
7 min_edge = None
8 min_weight = float('inf')
9 for e in E:
10 i, j = e
11 if (i in U and j not in U) or (j in U and i not in U):
12 if w[e] < min_weight:
13 min_weight = w[e]
14 min_edge = e
15 if min_edge is None: break # Disconnected graph
16 ET.add(min_edge)
17 if min_edge[0] in U: U.add(min_edge[1])
18 else: U.add(min_edge[0])
19 return (V, ET)
Laufzeit
Die Laufzeit ist $\mathcal O(|E||V|)$.
Idee Laufzeitverbesserung
Für jeden, noch nicht der Zusammenhangskomponente zugefügten, Knoten wird in dem Array $closest$ gespeichert, welcher Knoten aus der Zusammenhangskomponente am nächsten ist. Das reduziert den Aufwand für die Suche der minimalen Kante.
Für gegebene Menge $U\subset V$, wobei $U$ die Menge der Knoten ist, welche schon in der Zusammenhangskomponente ist, speichere für jeden (direkt erreichbaren) Knoten $v\in V\setminus U$ mit $Adj(v)\cap U\not=\emptyset$ den nächsten Nachbarn
$$closest[v]$$ab. D.h. einen Knoten $u\in U$ mit $w(\{u,v\})\leq w(\{u',v\})$ f.a. $u´\in U$. Beachte: $closest[v]=\bot$ bedeutet, dass der nächste Nachbar nicht definiert ist und $w(\{v,\bot\})=\infty$.
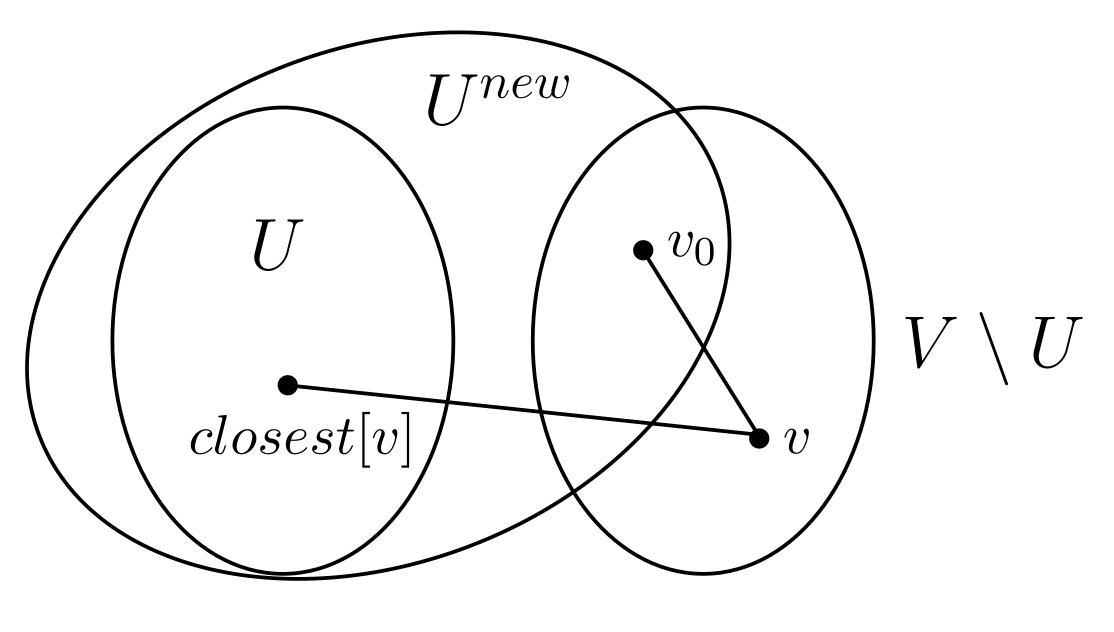
Updateschritt
Für einen Updateschritt wird zu jedem Knoten $v\in V\setminus U^{new}$ der Abstand zu dem neuen Knoten $v_0\in U^{new}$ und den bisherigen nächsten Nachbarn $closest[v]$.
Algorithmus
1def prim_jarnik_optimized(G, w):
2 V, E = G
3 n = len(V)
4 U = {0} # Using 0-based index (1 becomes 0)
5 ET = set()
6 closest = [None] * n
7 adj = [[] for _ in range(n)]
8 for (u, v) in E:
9 adj[u].append(v)
10 adj[v].append(u)
11 for v in range(1, n):
12 closest[v] = 0 if v in adj[0] else None
13 for _ in range(n-1):
14 min_edge = None
15 min_weight = float('inf')
16 for v in range(n):
17 if v not in U and closest[v] is not None:
18 edge_weight = w[(closest[v], v)] if (closest[v], v) in w else w[(v, closest[v])]
19 if edge_weight < min_weight:
20 min_weight = edge_weight
21 min_edge = (closest[v], v)
22 if min_edge is None: break
23 ET.add(min_edge)
24 v0 = min_edge[1]
25 U.add(v0)
26 for v in [x for x in adj[v0] if x not in U]:
27 edge_weight_new = w[(v0, v)] if (v0, v) in w else w[(v, v0)]
28 edge_weight_old = w[(closest[v], v)] if closest[v] is not None and (closest[v], v) in w else (w[(v, closest[v])] if closest[v] is not None else float('inf'))
29 if edge_weight_new < edge_weight_old:
30 closest[v] = v0
31 return (V, ET)
\begin{algorithm}
\caption{MST-Jarnik-Prim-A}
\begin{algorithmic}
\Input G=(V,E), w:E$\to\mathbb R$
\State Setze U = \{1\}, $E_T=\emptyset$, n = |V|;
\For{v = 2 \textbf{in} n}
\If{ v $\in$ Adj[1]}
\State closest[v] = 1;
\Else
\State closest[v] = $\bot$;
\EndIf
\EndFor
\For{k = 1 \textbf{ in } n-1}
\State Bestimme unter allen Kanten \{v, closest[v]\} mit v $\in$ V$\setminus$U und closest[v] $\not=\bot$ eine Kante e = \{$v_0$,$u_0$\} mit minimalen Gewicht;
\State $E_T = E_T \cup \{\text{e}\}$;
\State U = U $\cup$ \{$v_0$\};
\ForAll{v $\in$ (V$\setminus$U)$\cap$ Adj($v_0$)}
\If{w(\{$v_0$,v\}) < w(\{closest[v],v\})}
\State closest[v] = $v_0$;
\EndIf
\EndFor
\EndFor
\Return Baum T = (V,$E_T$)
\end{algorithmic}
\end{algorithm}
Laufzeit
Die Laufzeit beträgt $\mathcal O(|V|^2)$. Durch Fibonacci-Heaps kann die Laufzeit auf $\mathcal O(|E|+|V|\log|V|)$ reduziert werden.