Insertionsort

Einfache Sprache

Insertionsort ist ein Sortierverfahren, wobei das Feld in zwei Teile aufgeteilt wird. Ein sortierte und ein unsortierter Teil. Für das Sortieren wird ein Element aus dem unsortieren Teil gewählt und an die richtige Stelle im sortieren Teil eingefügt. Wiederhole das solange bis der unsortierte Teil leer ist.

Idee Insertionsort

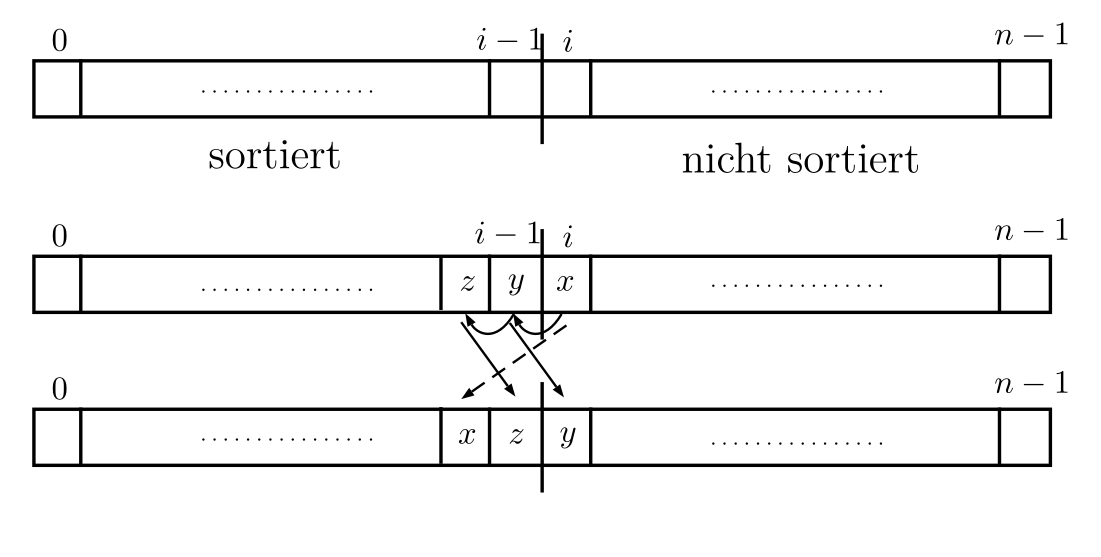
Halte einen sortierten (die ersten $i$ Elemente in $A$ von Position $0$ bis $i-1$) und einen nicht-sortierten Bereich in $A$ (die Elemente in $A$ von Position $i$ bis $n-1$) vor. Im $i$-ten Durchlauf (für $i$ von $1$ bis $n-1$) wähle das ($i+1$)-te Element $x=A[i]$ (auf Position $i$) aus dem noch nicht-sortieren Bereich und füge es durch Vertauschung an die richtige Stelle im sortierten Bereich.

Algorithmus

 1def insertion_sort(A):
 2    """
 3    Sorts an array in-place using Insertion Sort algorithm.
 4    Args:
 5        A: List of comparable elements to be sorted
 6    Returns:
 7        None: The input list is sorted in-place
 8    """
 9    n = len(A)
10    for i in range(1, n):
11        x = A[i]
12        j = i - 1
13        found = False
14        while not found and j >= 0:
15            if A[j] <= x:
16                found = True
17            else:
18                A[j + 1] = A[j]
19                j -= 1
20        A[j + 1] = x

Laufzeit

Die Laufzeit von Insertionsort beträgt $\mathcal O(n^2)$.

Aber ersetzt man die Lineare Suche in Zeile 9-16 durch Binäre Suche ersetzt verbessert sich die Laufzeit zu $\mathcal O(n\log n)$. Es wird der Part verbessert wo die Stelle für das nächste Element in dem sortierten Teil gesucht wird.