R-Baum

Einfache Sprache

Der R-Baum* ist die 2D-Generalisierung des B+-Baum. Kann aber auch in höheren Räumen angewendet werden.

Def. R-Baum

In einem R-Baum heißen die inneren Knoten Directory Pages und die Blätter Data Pages. Eine Directory page stellt ein Minimal umgebendes Rechteck (MBR) dar. Der MBR eines Kinderknotens liegt vollständig im MBR des Elternknoten. Eine Directory page hat zwischen $m$ und $M$ Kindknoten, wobei $m\leq\frac{M}{2}$. Die Datenelemente selbst sind nur in den Blattknoten gespeichert, so genante data pages. Die Wurzel ist auch ein (MBR), die den gesamten Datenraum umfässt.

Konstruktion eines R-Baums

Ein R-Baum wird mit folgenden Zielen konstruiert:

Minimierung der Überlappung von directory pages und
Minimierung der Fläche der einzelnen directory pages => Möglichst wenig leeren Raum abbilden. Die Konstruktion erfolgt nach Insertion-Strategien, wobei ein Split-Schritt gemacht werden muss falls ein Knoten mehr als $M$ Kindknoten hat.

Insertion Strategien

Es soll das Datenobjekt $A$ dem R-Baum hinzugefügt werden. Falls:

Falls $A$ vollständig in genau ein MBR einer directory page $D$ passt, so füge es dem Unterbaum $D$ hinzu.
Falls $A$ vollständig in das MBR mehrerer directory pages $D_1,\ldots,D_n$ passt, so füge es dem Unterbaum $D_i$ zu, dessen MBR die kleinst Fläche hat.
Sonst füge $A$ der directory page $D$ hinzu, dessen MBR durch das hinzufügen von $A$ am wenigsten wachsen würde. Der MBR von $D$ muss darauf hin angepasst werden.

Split Strategie

Falls durch eine Insertion der Knoten $K$ $M+1$ Kindknoten $R_0,\ldots,R_M$ hat, also $|K|=M+1$, so muss $K$ in zwei Knoten $K_1$ und $K_2$ geteilt werden so, dass $|K_1|\geq m$ und $|K_2|\geq m$.
Dazu gibt es z.B. den Quadratic Algorithm

Setze $K_1 \gets \emptyset$ und $K_2 \gets \emptyset$.
Finde die zwei Kindknoten $R_i,R_j$ mit $i,j\in[0,M]$ und $i\not=j$ so, dass wenn die beiden Kindknoten zu einer MBR gehören würden, der Leerraum $d(R_i,R_j)$ maximiert würde.$$d(R_i,R_j)=\textrm{area}(MBR(R_i\cup R_j))-\textrm{area}(R_i)-\textrm{area}(R_j)$$
Setze $K_1 \gets K_1 \cup \{R_i\}$ und $K_2 \gets K_2 \cup \{R_j\}$.
Falls alle $R_x$ zugeordnet oder alle übrigen $R_y,\ldots,R_z$ gebraucht werden um damit $K_1$ oder $K_2$ die mindest Anzahl $m$ an Kindsknoten erfüllt => Abbruch!
Sonst wähle das nächste $R_x$ und füge es dem Knoten hinzu, der dadurch den geringsten Anstiegt des MBR erfährt. Bei Patt dem Knoten mit weniger Einträgen.

Suche in einem R-Baum

Bei Entfernungsabfragen ergibt sich folgender Algorithmus, wobei $pa$ die Wurzel des R-Baums, $q$ das gesuchte Element und $\varepsilon$ die Toleranz ist. Dabei gibt $x.\textrm{loadPage}()$ die Kindknoten von $x$ wieder. Diese können entweder data pages oder directory pages sein.

\begin{algorithm}
\caption{Entferungsabfrage R-Baum}
\begin{algorithmic}
\Input $\textrm{page adress }pa,\textrm{query object  }q,\textrm{tolerance }\varepsilon$
\Procedure{RQ-Index}{$pa,q,\varepsilon$}
\State $r\gets\emptyset$
\State $p \gets pa.\textrm{loadPage}()$
\If{$p.\textrm{isDataPage}()$}
	\For{$i = 0$ to $p.\textrm{size}()$}
		\State $o \gets p.\textrm{getObject}(i)$
		\If{$\textrm{dist}(q,o)\leq\varepsilon$}
			\State $r\gets r\cup o$
        \EndIf
    \EndFor
\Else
	\For{$i = 0$ to $p.\textrm{size}()$}
		\If{\Call{Mindist}{$q,p.\textrm{getRegion}(i)$} $\leq\varepsilon$}
			\State $r\gets r\;\cup\;$\Call{RQ-Index}{$p.\textrm{childPage}(i),q,\varepsilon$}
        \EndIf

    \EndFor
\EndIf
\return $r$
\EndProcedure
\end{algorithmic}
\end{algorithm}

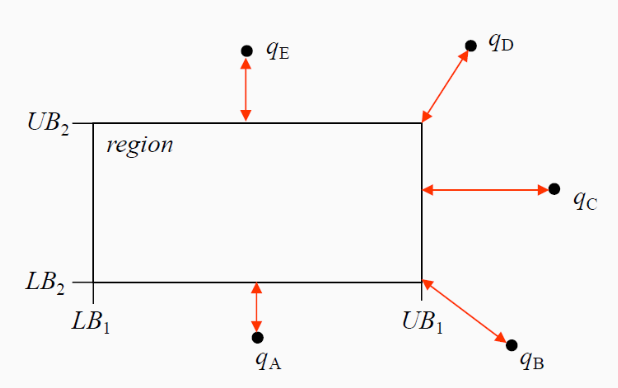
MINDIST für $L_2$ Norm

Die die $L_2$ Norm ergibt sich
$$\textrm{MINDIST}(R,q)=\sqrt{\sum_{0\leq i\leq d}\begin{cases}(r.\textrm{LB}_i-q_i)^2 & \textrm{if} & q_i< r.\textrm{LB}_i\\0 & \textrm{if} & r.\textrm{LB}_i \leq q_i\leq r.\textrm{UB}_i\\(r.\textrm{LB}_i-q_i)^2 & \textrm{if} & q_i> r.\textrm{UB}_i\end{cases}}$$

Bei KNN ergibt sich folgender Algorithmus

\begin{algorithm}
\caption{KNN R-Baum}
\begin{algorithmic}
\Input $\textrm{page adress }pa,\textrm{query object  }q,\textrm{Nachbaranzahl }k$
\Procedure{kNN-Index-APL}{$pa,q,k$}
\State $r \gets$ List of $(d\in\mathbb R,q\in\textrm{Object})$ Orderd by $d$ ascending
\State $\textrm{apl} \gets$ List of $(d\in\mathbb R,a\in\textrm{DiskAdress})$ Orderd by $d$ ascending
\State $a\gets[(0.0,pa))]$
\State $pd \gets [(+\infty,null),\ldots,(+\infty,null))]$
\Comment{$r.\textrm{length}() = k$}
\State $pd \gets +\infty$
\While{not $\textrm{apl}.\textrm{isEmpty}()$ and $\textrm{apl}.\textrm{getFirst}().d\leq\textrm{prundist}$}
	\State $p\gets \textrm{apl}.\textrm{getFirst}().a.\textrm{loadPage}()$
	\State $\textrm{apl}.\textrm{deleteFirst}()$
	\If{$p.\textrm{isDataPage}()$}
		\For{$i = 0$ to $p.\textrm{size}()$}
			\If{$\textrm{dist}(q,p.\textrm{getObject}(i))\leq pd$}
				\State $r.\textrm{removeLast}()$
				\State $r.\textrm{insert}((\textrm{dist}(q,p.\textrm{getObject}(i)),p.\textrm{getObject}(i)))$
				\State $pd\gets rp.\textrm{getLast}().d$
            \EndIf 
        \EndFor
    \Else
		\For{$i = 0$ to $p.\textrm{size}()$}
			\If{$\textrm{MINDIST}(q,p.\textrm{getRegion}(i))\leq pd$}
				\State $\textrm{apl}.\textrm{insert}((\textrm{MINDIST}(q,p.\textrm{getRegion}(i)), p.\textrm{childPage}(i))$
			\EndIf
		\EndFor
	\EndIf
\EndWhile
\return $r$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Home: