Reguläre Sprache
Einfache Sprache
Als reguläre Sprache bezeichnet man die Sprachen die von einem Endlicher Automat erkannt (erkennen) werden und als Regulärer Ausdruck dargestellt werden können.
Def. Reguläre Sprache
Reguläre Sprachen können auf verschiedener Weise definiert werden
Mit einer Sequenzielle Funktion
Def. Reguläre Sprache mit seq. Funktion
Eine Sprache $L$ von Wörtern über einem Alphabet $A$ heißt regulär, wenn es eine Sequenzielle Funktion $f \colon A^* \rightharpoonup B^*$ gibt, deren Definitionsbereich $L$ ist, d.h., wenn $L = \text{dom}(f)$ gilt.
Das heißt das die Sequenzielle Funktion also für alle Eingaben definiert sein muss.
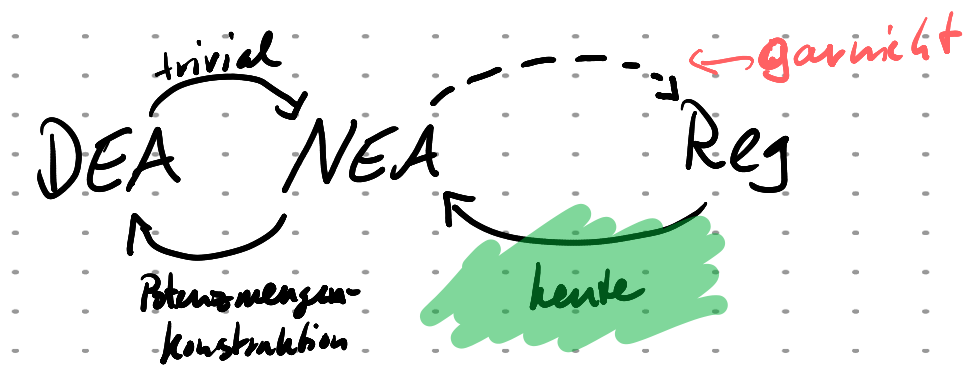
Mit DEA
Def. Reguläre Sprache mit DEA
Eine Sprache $L$ heißt regulär, falls ein DEA $\mathcal A$ ex., sodass $L(\mathcal A)=L$.
Mit regulärem Ausdruck
Def. Reguläre Sprache mit DEA
Eine Sprache $L$ heißt regulär, wenn $L=L(R)$ für einen Regulärer Ausdruck $R\in Reg_A$.
Eigenschaft von reguläre Sprachen