Traveling Salesman Problem

Einfache Sprache

Es ist ein Entscheidungsproblem bei dem eine Menge an Knoten mit Verbindungen, die jeweils bestimmte Entfernungen haben. Dies könnte bspw. Städte und Straßen darstellen. Es wird eine Rundreise gesucht bei den alle Knoten besucht werden und dabei die zurückgelegt Distanz minimiert wird.

Problemstellung:

Gegeben: Eine Menge $V=\{1,\ldots,n\}$, Distanzen (Gewichte) $d(i,j)\in \mathbb Z^+\cup\{\infty\}$ für alle $i,j\in\{1,\ldots,n\}$. Gesucht: Eine minimale Rundreise, die jeden Knoten genau einmal besucht. _ Formal:_ Die Lösung ist eine Permutation $\Pi$ von $\{1,\ldots,n\}$, wobei die Länge der Tour $\sum_{i=1}^n d(\Pi(i),\Pi(i+1))$ mit $\Pi(n+1)=\Pi(1)$ ist. Hier ist $\Pi(i)$ der $i$-te Knoten in der Rundreise.

Satz: TSP

Das Entscheidungsproblem zu einem Traveling Salesman Problem, ob eine Rundreise mit Länge $\leq L$ existiert, ist NP-vollständig.

Reduktionsbeweis aufschreiben -> vom Hamiltonkreis Problem #TODO

Exakte Lösung

Mithilfe von Dynamische Programmierung

Idee Lösung mit DP

Berechne Werte $C(S,k)$ für alle Teilmengen $S\subseteq\{2,\ldots, n\}$ und jedes Element $k\in S$, wobei $C(S,k)$ die minimale Länge einer Tour von Knoten $1$ über alle Knoten in $S$ ist, die bei $k$ endet.

	\begin{algorithm}
	\caption{TSP}
	\begin{algorithmic}
	\Input Gewichteter Graph $G=(V,E)$
	\Procedure{TSP-DP}{$G$}
	\State Für alle Teilmengen $S\subseteq\{2,\ldots,n\}$ mit $S=\{k\}$ gilt: $C(\{k\},k)=d(1,k)$
	\State Für alle Teilmengen $S$ mit $|S|\geq 2$ gilt: $C(S,k) = \min_{m\in S\setminus \{k\}}\{C(S\setminus\{k\},m)+d(m,k)\}$
    \EndProcedure
	\end{algorithmic}
	\end{algorithm}

Example

Die Tour at die Länge $C(S, k) = C(S \setminus \{k\}, m) + d(m, k)$.

Für jedes $C(S,k)$ müssen aber die Knoten abgespeichert werden, die die Kosten zusammensetzen.Nur so kann man am Ende die Tour rekursiv erzeugen. Das benötigt $\mathcal O(n2^n)$ Einträge. Die Laufzeit beträgt $\mathcal O(n^22^n)$.

Approximative Lösung

Lösungsansatz 1

Achtung: funktioniert nur wenn die Dreiecksungleichung erfüllt ist.

Mithilfe von Eulerkreisen

Idee TSP mit Eulerkreis

Berechne zuerst einen MST auf dem Graph. Verdoppele jede Kante in ihm und suche dann einen Eulerkreis. In dem Weg kürze schon besuchte Knoten heraus und erhalte so eine aproximierte Rundreise $R$ mit der Güte von Approximationsalgorithm

	\begin{algorithm}
	\caption{TSP mit Eulerkreis}
	\begin{algorithmic}
	\Input Gewichteter Graph $G=(V,E)$
	\Procedure{TSP-EK}{$G$} 
	\State Berechne einen \textbf{minimalen spannenden Baum} $T$ des Graphen $G$.
	\State Konstruiere einen \textbf{Multigraphen} $M$ aus $T$ durch Verdoppeln aller Kanten.
	\State Bestimme einen \textbf{Eulerkreis} $K$ in $M$.
	\State Bestimme eine \textbf{Rundreise} $R$ aus $K$ durch Abkürzungen.
	\Return Rundreise $R$.
	\EndProcedure
 	\end{algorithmic}
	\end{algorithm}

Satz: Güte von $\textrm{TSP-EK}$

Der Algorithmus $\textrm{TSP-EK}$ hat eine multiplikative Güte $2$.

Beispiel von $\textrm{TSP-EK}$

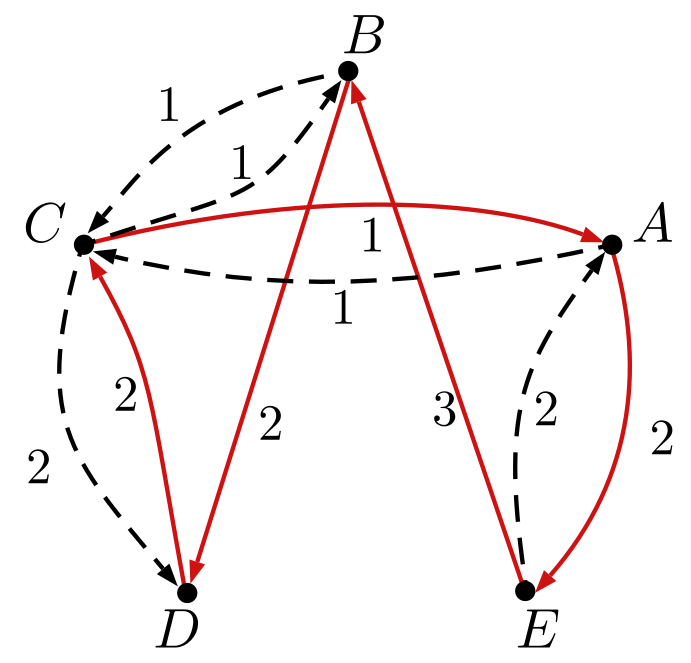
Sei gewichteter Graph mit $V= \{A,B,C,D,E\}$ und folgenden Kanten gegeben: Es wird zuerst ein MST berechnet mit Länge $6$: Alle Kanten des minimalen Spannbaums werden verdoppelt: Auf diesem Multigraphen wird nun ein Eulerkreis berechnet mit $K=[C,A,E,A,C,B,C,D,C]$ und Länge $12$. Durch abkürzen wird dann die Rundreise $R=[C,A,E,B,D,C]$ wiefolgt:

Lösungsansatz 2

Achtung: funktioniert nur wenn die Dreiecksungleichung erfüllt ist. Funktioniert mithilfe von Eulerkreisen und matching

Idee TSP mit Eulerkreis

Berechne zuerst einen MST auf dem Graph. Verdoppele jede Kante in ihm und suche dann einen Eulerkreis. In dem Weg kürze schon besuchte Knoten heraus und erhalte so eine aproximierte Rundreise $R$ mit der Güte von Approximationsalgorithm

	\begin{algorithm}
	\caption{TSP mit PM}
	\begin{algorithmic}
	\Input Gewichteter Graph $G=(V,E)$
	\Procedure{TSP-EK}{$G$} 
	\State Berechne einen \textbf{minimalen spannenden Baum} $T$ des Graphen $G$.
	\State Bestimme die Menge $X$ der Knoten in $T$, die ungeraden Grad haben
	\State Bilde den vollständigen Graphen $H$ auf $X$ mit Gewichten aus $E$
	\State Bestimme ein perfektes Matching $P$ in $H$ mit minimalem Gewicht.
	\State Bilde den Multigraphen $M$, der aus $T$ durch Hinzufügen aller Kanten aus $K$ entsteht.
	\State Bestimme einen Eulerkreis $C$ in $M$.
	\State Bestimme eine Rundreise $R$ aus $C$ durch Abkürzungen.
	\Return Rundreise $R$.
	\EndProcedure
 	\end{algorithmic}
	\end{algorithm}

Satz: Güte von $\textrm{TSP-PM}$

Der Algorithmus $\textrm{TSP-PM}$ hat eine multiplikative Güte $\frac{3}{2}$.

Beispiel mit $\textrm{TSP-PM}$

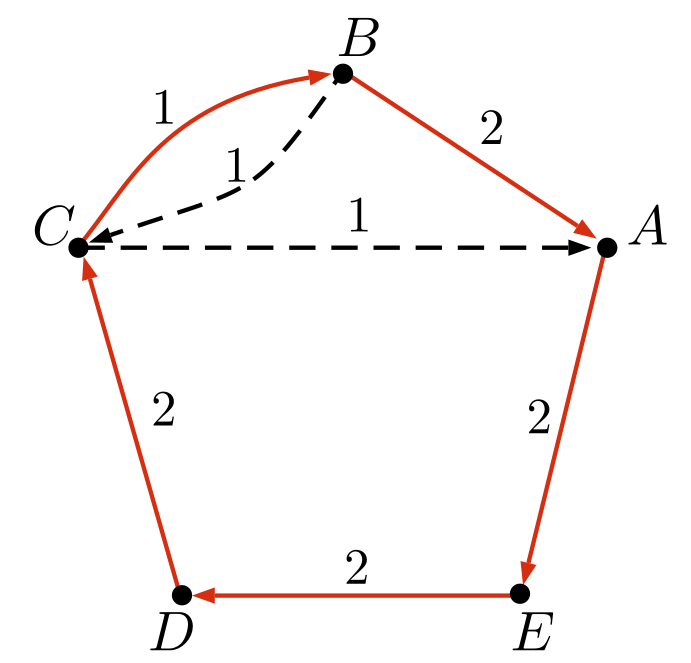
Berechne zuerst den MST in dem Graphen. Hier blau eingezeichnet: Baue aus allen Knoten des minimalen Spannbaums mit ungeradem Grad (also ungerade Anzahl an Kanten) einen Graph (hier $H$ genannt) mit allen dazugehörigen kannten. Berechne auf $H$ das perfekte Matching $K$. Füge die Kanten aus $K$ in den minimalen Spannbaum ein und berechne einen Eulerkreis $C$. Hier $C=[C,B,C,A,E,D,C]$ Durch abkürzen wird dann die Rundreise $R=[C,B,A,E,D,C]$:

Home: