Zeitkomplexität

Einfache Sprache

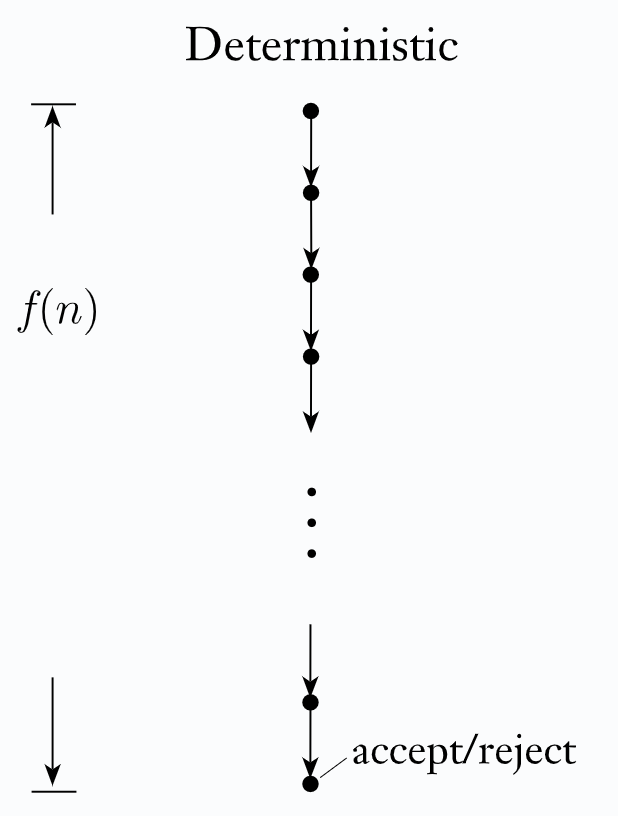
Def. deterministische Zeitkomplexität

Sei $M$ eine Deterministische Turingmaschine die auf allen Eingaben hält. Die Zeitkomplexität (auch Laufzeit) ist die Funktion $f:\mathbb N\to\mathbb N$, wobei $f(n)$ die maximale Anzahl an Schritten ist, die $M$ auf beliebigen Eingabe der Länge $n$ braucht. Falls $f(n)$ die Zeitkomplexität von $M$ ist, sagen wir auch das $M$ in der Zeit $f(n)$ läuft und das $M$ eine $f(n)$ Laufzeit-Turingmaschine. Normalerweise ist $n$ die Länge der Eingabe.

Zur Quantifizierung der Zeitkomplexität dienen die Landau-Symbole.

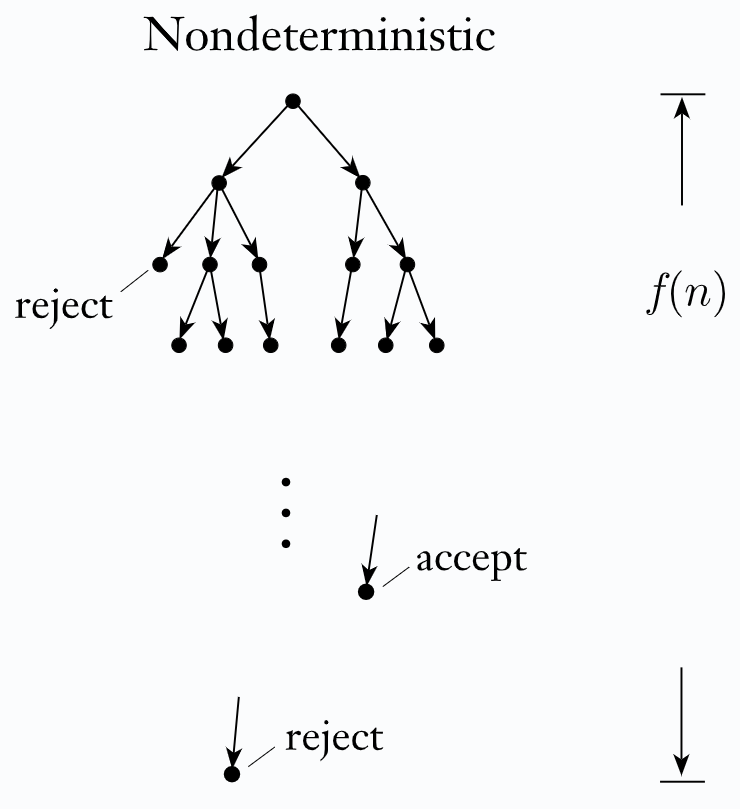
Def. nichtdeterministische Zeitkomplexität

Sei $N$ eine Nichtdeterministische Turingmaschine, die eine Sprache entscheidet. Die Zeitkomplexität von $N$ ist die Funktion $f:\mathbb N\to \mathbb N$, wobei $f(n)$ die maximale Anzahl an Schritten aller möglichen Berechnungen ist.

Laufzeit eines Algorithmus

Def. Laufzeit eines Algorithmus

Sei $\Sigma$ ein Alphabet, $x\in\Sigma^*$ und $A$ ein Algorithmus arbeitet auf $\Sigma^*$.

Die Laufzeit von $A$ zur Eingabe $x$ (gegeben durch die von dem Algorithmus ausgeführten Operationen) wird durch $T_A(x)$ bezeichnet. Die Worst Case Laufzeit zu Eingaben der Größe $n$ ist

$$T_A(n) = \max\left\{T_A(x)|x\in\Sigma^* , |x| = n\right\}.$$

Ist der Algorithmus aus dem Kontext klar wird gelegentlich auch nur $T(n)$ verwendet.