Satz 3SAT is poly reduzierbar auf CLIQUE
Einfache Sprache
Der Satz zeigt wie man eine Formel in einen Graphen transformieren kann so, dass genau dann wenn die Formel 3SAT erfüllt der Graph auch CLIQUE erfüllt.
Def. Satz 3SAT is poly reduzierbar auf CLIQUE
3SAT ist polynomial reduzierbar auf CLIQUE.
Beweis: Sei $\phi$ eine Aussagenlogischen Formel in KNF mit $k$ Klauselen so, dass
$$\phi = (a_1\lor b_1\lor c_1)\land\ldots\land(a_k\lor b_k\lor c_k)\;.$$Die Polynomialzeitreduktion $f$ generiert eine Zeichenkette $\langle G,k\rangle$, wobei $G$ ein Graph ist, wie folgt:
Die Knoten von $G$ sind in $k$ Gruppen $t_1,\ldots,t_k$, genannt triplets, mit jeweils 3 Knoten aufgeteilt. jedes triplet gehört zu einer Klausel in $\phi$ und jeder Knoten in dem triplet gehört zu einer Variable in der Klausel. Wir benennen jeden Knoten nach dieser Variable. Alle Knoten sind miteinander Verbunden außer zwei Arten von Knoten:
- Zwischen Knoten im selben triplet gibt es keine Kante.
- Zwischen Knoten die sich widersprechen gibt es keine Kante. Z.B. zwischen $x_2$ und $\overline{x_2}$.
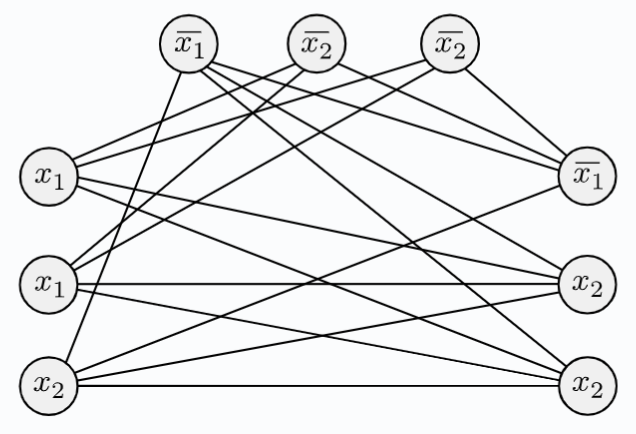
Beispiel Konstruktion
Geben die Formel $\phi = (x_1\lor x_1\lor x_2)\land(\overline{x_1}\lor \overline{x_2}\lor \overline{x_2})\land(\overline{x_1}\lor x_2\lor x_2)$ baut $f$ folgenden Graphen:
Jetzt müssen wir noch zeigen das die Konstruktion funktioniert.
$$\left[\mathrm{Z\kern-.5em\raise-0.6ex\hbox{Z}}\; \phi\text{ ist erfüllbar}\iff G \text{ hat eine $k$-clique}\right]$$“$\Rightarrow$”: Nehme an das $\phi$ eine erfüllende Belegung hat. In der Belegung muss mind. eine Literal in jeder Klausel wahr sein. Falls mehrere Literale wahr sind wähle zufällig eines aus. Wir wählen nun die entsprechenden Knoten aus $G$ aus. Wir haben genau $k$ Knoten. Alle Knoten sind miteinander Verbunden weil kein Paar die oben genanten Ausnahmen erfüllt. (1) Sie können nicht aus dem gleichen Triplet sein, da wir nur einen Knoten pro triplet ausgewählt haben. (2) Sie können sich nicht widersprechen, weil die variablen die wir ausgewählt haben alle Wahr sind bezüglich der Belegung. Daher hat $G$ einen $k$-Clique. “$\Leftarrow$”: Nehme an $G$ hat eine $k$-Clique. Dann können keine zwei Knoten in dem selben Triplet sein, da die Knoten in einem Triplet nicht durch Kanten miteinander Verbunden sind. Also enthält jedes der $k$ Triplets genau einen der $k$ Knoten aus $k$-Clique. Für die Belegung von $\phi$ setzten wir alle Variablen auf Wahr die auch in dem k-Clique sind. Das ist erlaubt weil keine sich widersprechenden Variablen miteinander Verbunden sind und daher auch nicht gemeinsam Teil der $k$-Clique sein können. Diese Belegung ist eine Erfüllende Belegung für $\phi$, da jedes triplet einen Knoten aus $k$-Clique enthält, also hat jede Klausel eine Literal was Wahr ist. Daher ist $\phi$ erfüllbar.