Satz EQ-ROBP in BPP
Einfache Sprache
Def. Satz EQ-ROBP in BPP
EQ-ROBP $\in$ BPP.
Wir können nicht jede mögliche Variablenbelegung testen, da es mit $2^m$ verschiedenen Möglichkeiten zu viele gibt so, dass dieser Ansatz in EXPTIME landen würde.
Idee: Wir wählen zufällige Variablenbelegungen und testen die zwei ROBP auf diesen auf bestimmter weise. Wir können dann zeigen, dass wenn beide ROBP nicht äquivalent sind, dann auch die zufälligen Auswertungen nicht gleich sind.
Beweis: Wir beschriften die Knoten und Kanten der ROBP wie folgt mit Polynomen:
- Der Startknoten ist mit der konstante Funktion $1$ beschriftet.
- Falls ein Knoten $x$ mit dem Polynom $p$ beschriftet ist, dann wir die ausgehende $1$-Kante mit $xp$ beschriftet und die ausgehende $0$-Kante mit $(1-x)p$ beschriftet.
- Falls die die alle eingehende Kanten eines Knotens $x$ beschriftet sind, dann beschrifte $x$ mit der Summe aller Polynome der eingehenden Kanten.
- Das Polynom mit das der Ausgabekonten $0$ beschriftet wird, ist das Polynom des ROBP.
Sei $\mathcal F$ ein endlicher Körper mit mindestens $3m$ Elementen. Dann arbeitet die Probabilistische Turingmaschine die EQ-ROBP in Polynomialzeit entscheidet wie folgt für die Eingabe zweier ROBP:
- Wähle $a_1,\ldots,a_m$ zufällig aus $\mathcal F$.
- Werte die zugewiesenen Polynome $p_1$ und $p_2$ für $a_1$ bis $a_m$ aus.
- Falls $p_1(a_1,\ldots,a_m) = p_2(a_1,\ldots,a_m)$, akzeptiere. Sonst verwerfe.
Lemma 1
Lemma Nullstellen eines d-grad Polynoms
Behauptung: Für jedes $d\leq 0$ hat ein Polynom von Grad $d$ gegeben einen einzelne Variable $x$ entweder höchstens $d$ Nullstellen oder ist unabhängig von $x$ immer Null.
Beweis: Induktion über $d$.
Induktionsanfang. Sei $d = 0$. Ein Polynom mit Grad $0$ ist Konstant. Wenn die Konstante nicht $0$ ist, dann hat das Polynom keine Nullstellen. Ist die Konstante $0$, dann is es unabhängig von $x$ immer Null. Induktionsschritt. Sei $(d-1)\geq 0$ und $d-1$ hat für $x$ höchstens $d-1$ Nullstellen oder ist unabhängig von $x$ immer Null. Sei $p$ ein Polynom mit Grad $d$ was nicht Null ist und eine Nullstelle bei $a$ hat. Dann teilt das Polynom $x-a$ das Polynom $p$ so, dass es kein Rest gibt. Also ist $x-a$ ein Faktor von $p$ so, dass $p= (x-a)*q$ für ein bestimmtest Polynom $q$. Daher ist $p/(x-a)$ ein Polynom mit Grad $d-1$. Hier wenden wir die Induktionshypothese an und schließen dadurch p höchstens $d$ Nullstellen hat.
Beispiel
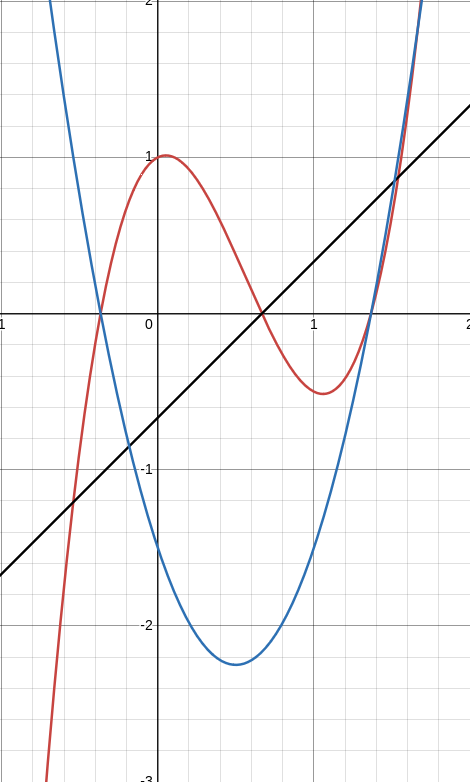
Gegeben das Polynom $f(x)=3x^{3}-5x^{2}+0.5x+1$ (rot). Es hat eine Nullstelle bei $a = 0,\bar 6$. Die Funktion $g(x) = x - a = x-0,\bar 6$ ist schwarz. Sie geht durch die Nullstelle. Die Funktion $h(x)=\frac{f(x)}{g(x)}$ in blau geht durch die restlichen zwei Nullstellen.