Deutsch-Jozsa Algorithm

Einfache Sprache

Man hat eine Funktion, welche als Input einen Bit-Vektor hat. Sie soll herausfinden ob in dem Input alle Bits gleich sind oder genau Hälfte 1 und die andere Hälfte 0. Es wird garantiert das es eines von beidem ist.

Problemdefinition

Gegeben eine balanced oder constant boolesche Funktion $f$. Bestimmte ob $f$ balanced oder constant ist. Für $n>0$ ist einer booleschen Funktion $f:\{0,1\}^n\to\{0,1\}$:

balanced wenn $|\{b\in\{0,1\}^n:f(b)=0\}|=|\{b\in\{0,1\}^n:f(b)=1\}|$,

constant wenn $f(b)=f(b')$ für alle $b,b'\in\{0,1\}^n$.

Deterministischer Algorithmus

Checke die ersten $2^{n-1}+1$ Einträge ab.

Check zwei Zufällige Einträge der Eingabe ab. Wenn sie gleich sind dann sagen wir das die Eingabe constant ist, sonst das sie balanced ist. Wenn der Bit-Vektor constant ist, dann Stimmt unsere Algorithmus. Andernfalls liegen wir mit 50% Richtig. $\Rightarrow$ Die Idee is dann durch $m$-faches Wiederholen geht die Fehlerquote gegen 0

Quanten Algorithmus

Idee Deutsch-Jozsa

Idee für deutsch-jozsa fomulieren #TODO

	\begin{algorithm}
	\caption{Deutsch-Jozsa Algorithm}
	\begin{algorithmic}
	\Input build-in oracle $O_{f,\pm}$ for a balanced or constant $f:\{0,1\}^n\to \{0,1\}$        
	\Comment{We use \textbf{integer notation}}
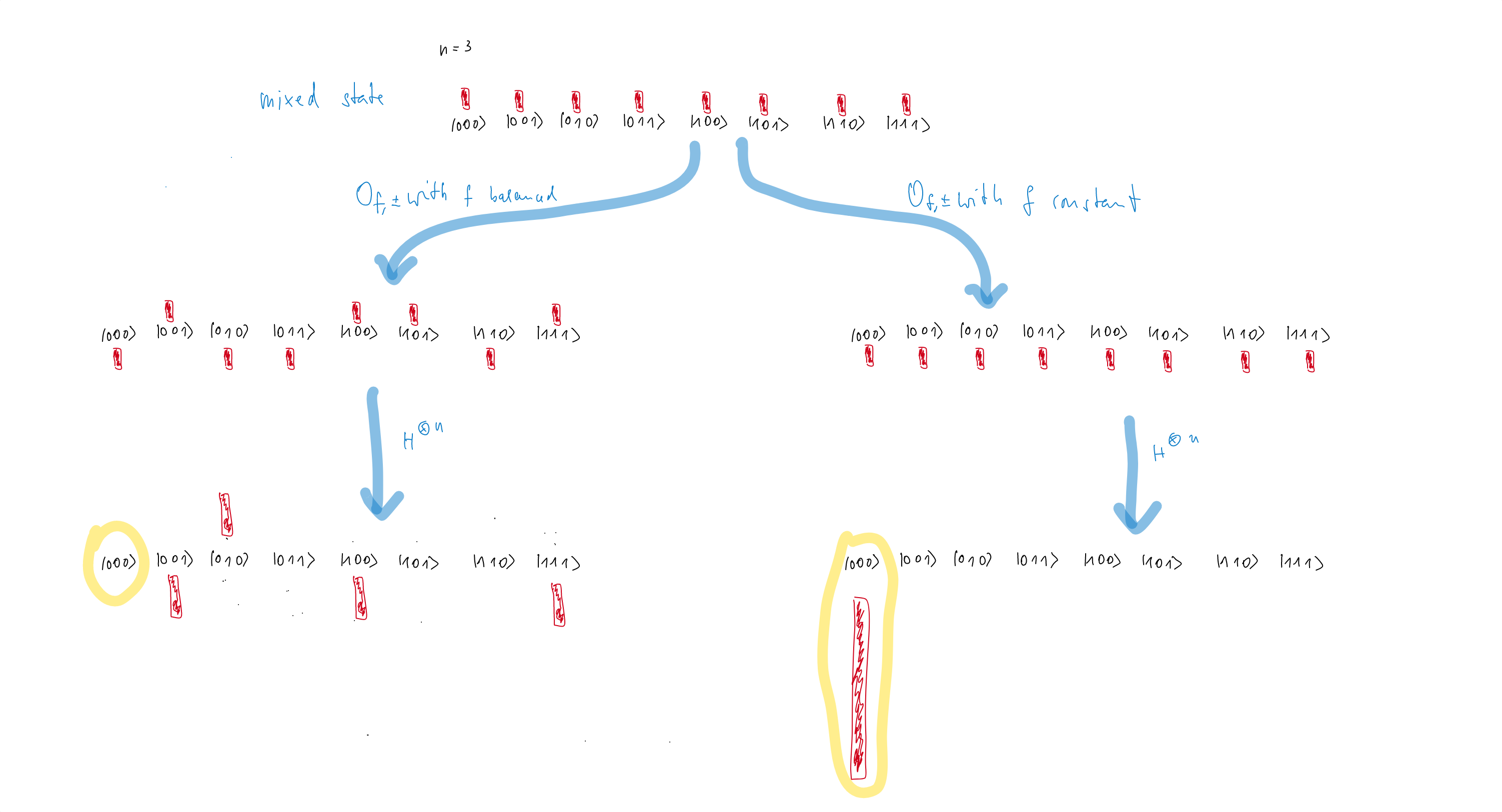
	\Procedure{Deutsch-Josza}{$O_{f,\pm}$}
	\State Initialize with $|0^n\rangle$.
	\Comment{State $\varphi_0$: $|0^n\rangle$}
	\State Apply $H^{\otimes n}$.
	\Comment{State $\varphi_1$: $\frac{1}{\sqrt{2^n}}\sum_{i<2^n}|i\rangle$}
	\State Apply $O_{f,\pm}$.
	\Comment{State $\varphi_2$: $\frac{1}{\sqrt{2^n}}\sum_{i<2^n}(-1)^{f(i)}|i\rangle$}
	\State Apply $H^{\otimes n}$.
	\Comment{State $\varphi_3$: $\frac{1}{2^n}\sum_{j<2^n}\left (\sum_{i<2^n}(-1)^{f(i)}(-1)^{i\odot j}\right )|j\rangle$}
	\State Measure $b_0,\ldots,b_{n-1}$.
	\If{$b_0\lor\ldots\lor b_{n-1}$}
	\Return balanced
	\Else
	\Return constant
    \EndIf
    \EndProcedure
	\end{algorithmic}
	\end{algorithm}

Erklärung

Von $\varphi_2$ nach $\varphi_3$:

$$\begin{aligned} &H^{\otimes n}\left (\frac{1}{\sqrt{2^n}}\sum_{i<2^n}(-1)^{f(i)}|i\rangle\right )\\ =&\frac{1}{\sqrt{2^n}}\sum_{i<2^n}(-1)^{f(i)}H^{\otimes n}|i\rangle &|\text{Linearität}\\ =& \frac{1}{\sqrt{2^n}}\sum_{i<2^n}(-1)^{f(i)}\left(\frac{1}{\sqrt{2^n}}\sum_{j<2^n}(-1)^{i\odot j}|j\rangle\right)&|\text{Lemma}\\ =& \frac{1}{2^n}\sum_{i,j<2^n}(-1)^{f(i)}(-1)^{i\odot j}|j\rangle &|\text{Arithmetik}\\ =& \sum_{j<2^n}\frac{1}{2^n}\left (\sum_{i<2^n}(-1)^{f(i)}(-1)^{i\odot j}\right )|j\rangle&|\text{Arithmetik} \end{aligned}$$

Wenn man für $j= |0^n\rangle$ einsetzt sieht man das die Amplitude $\frac{1}{2^n}\sum_{i<2^n}(-1)^{f(i)}$ ist. Die Amplitude ist also

$1$ wenn $f(i)=0$ für alle $i<2^n$, (constant $0$)
$-1$ wenn $f(i)=1$ für alle $i<2^n$, (constant $1$)
0 wenn $f$ balanced ist. In anderen Worten:
Wenn $f$ constant ist, dann ist der Zustand $|0^n\rangle$ oder $-|0^n\rangle$.
Wenn $f$ balanced ist, dann damm ist die Amplitude von $|0^n\rangle$ gleich $0$.

Lemma

Für alle $b\in\{0,1\}^n$,

$$H^{\otimes n}|b\rangle = \frac{1}{\sqrt{2^n}}\sum_{c\in\{0,1\}^n}(-1)^{b\odot c}|c\rangle\;,$$

wobei $\odot$ für das Skalarprodukt von Bit-Vektoren steht. Also $b\odot c = \sum_{i

Alternativ für $|\varphi\rangle = \sum_{b\in\{0,1\}^n}\alpha_b|b\rangle$ and $c\in\{0,1\}^n$,

$$\langle H^{\otimes n}|\varphi\rangle| |c\rangle\rangle = \frac{1}{\sqrt{2^n}}\sum_{b\in\{0,1\}^n}(-1)^{b\odot c}\alpha_b\;.$$

Example

Home: