Grover-Algorithmus

Einfache Sprache

Man bekommt eine Funktion welche nur für eine einzige Eingabe $1$ ausgibt und sonst $0$. Gesucht ist die Eingabe die $1$ als Ausgabe erzeugt.

Grover’s Problem

Gegeben sei eine einzigartige Funktion, find die Lösung.

Deterministischer Algorithmus

Im Worst case sind $2^{n}-1$ Evaluationen von $f$ nötig.

Randomisierter Algorithmus

Auch Randomisierung hilft uns hier nicht weiter.

Quanten Algorithmus

Idee Grover

Wir starten mit dem $|v\rangle = |+^n\rangle$ welcher gleich weit von der Lösung ($|a\rangle\in\{0,1\}^n$) und allen anderen basis-Vector ist. also die superposition aus allen Zuständen. Als zweiten Vektor nehmen wir die superposition aus allen Zuständen ausgeschlossen der Lösung. Diesen Zustand erhält man in dem man indem man das Orakel auf $|+^n\rangle$ anwendet. Dadurch wird die amplitude des Basis Vectors der Lösung auf 0 gesetzt während die anderen gleich verteilt bleiben.

Also

Die Vektoren $|a\rangle, |v\rangle$ und $|u\rangle$ liegen auf einer Ebene $e$. Durch iteratives Rotieren eines Vektors mit Hilfe des double reflection principles nähert sich der Vektor auf der Ebene $e$ der Lösung $|a\rangle$. Grob kann es so veranschaulicht werden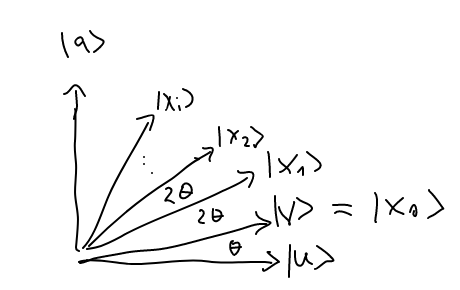

	\begin{algorithm}
	\caption{Grover-Algorithmus}
	\begin{algorithmic}
	\Input build-in oracle $O_{f,\pm}$ for a unique boolean function $f:\{0,1\}^n\to \{0,1\}$
	\Procedure{Grover}{$O_{f,\pm}$}
	\State $\theta = \measuredangle(|u\rangle,|v\rangle) = \sqrt{1-\frac{1}{2^n}}$
	\State $r = \lfloor \frac{\pi}{4\theta}-\frac{1}{2}\rceil$
	\State Initilize $|v\rangle$ and denote it by $|x_0\rangle$
	\State Apply $(VU)^r$
	\Comment{Reflect $r$ times first around $|u\rangle$ and then around $|v\rangle$ }
	\State Measure $b_0,\ldots,b_{n-1}$
	\If{$f(b)=1$}
		\Return $b$
	\Else
		\Return Failed
    \EndIf
    \EndProcedure	    
	\end{algorithmic}
	\end{algorithm}

Erkärung

Werte $\theta$ und $r$

$\theta = \measuredangle(|u\rangle,|v\rangle$ is der Winkel zwischen $|u\rangle$ und $|v\rangle$ um den $|x_i\rangle$ rotiert wird. $r$ ist die Anzahl der Rotationen die Nötig sind um in der Nähe von $|a\rangle$ zu sein. Da $|u\rangle$ unserer Ausgangspunkt ist und wird zu $|a\rangle$ wollen was orthogonal (Orthogonalität) zu $|u\rangle$ ist, müssen wir den $|u\rangle$ genau $90\degree$ rotieren. Das sind $\pi/2$ in Bogenmaß. Wir müssen also $r$ so wählen das $r$-fache Rotation $\theta$ gleich $\pi/2$ ist.

$(VU)^r$

$U$ ist die Reflexion durch $|a\rangle^\bot$ und ist implementiert mit $O_{f,\pm}$:

1. $O_{f,\pm}|a\rangle=-|a\rangle$
2. $O_{f,\pm}|b\rangle=|b\rangle$ für alle $b\in\{0,1\}^n$ mit $b\not=a$. 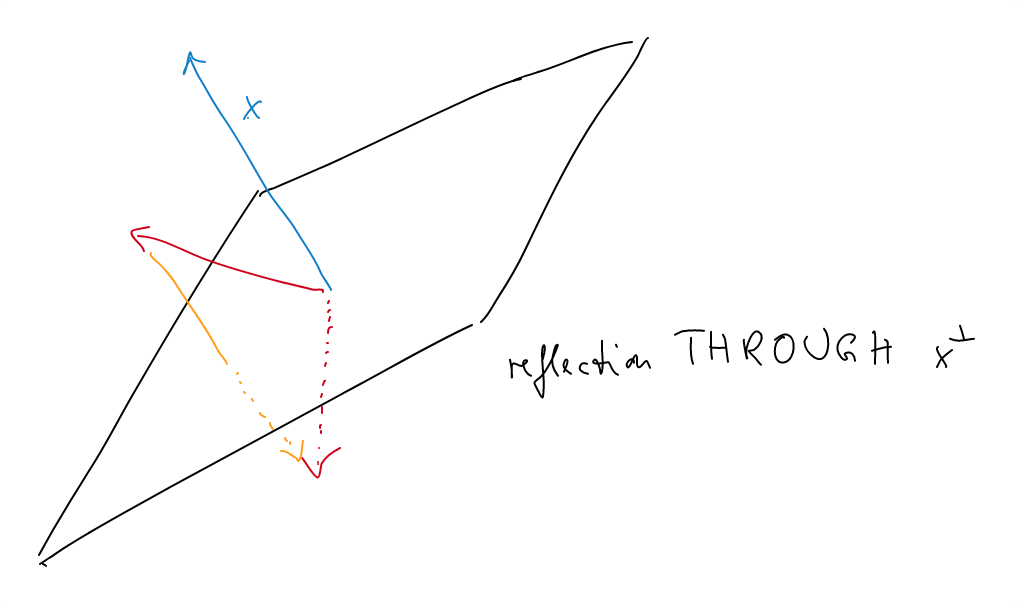$V$ ist die Reflextion um $|v\rangle$ und ist gegeben durch $$V|b\rangle=H^{\otimes n}O_gH^{\otimes n}|b0\rangle\quad  \forall b∈\{0,1\}^n$$ wobei $g:\{0,1\}^n\to\{0,1\}$ definiert durch $g(0^n) = 0$ und sonst $1$.