Matrixmultiplikation

Einfache Sprache

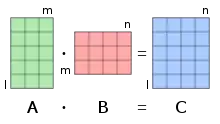
Bei der Matrixmultiplikation werden zwei Matrizen miteinander multipliziert um eine neue Matrix zu erhalten. Das funktioniert nur wenn die Spaltenzahl der ersten Matrix gleich der Zeilenzahl der zweiten Matrix ist.

Def. Matrixmultiplikation

Sei $R$ ein Ring, z.B. die Reellen Zahlen. Die Matrixmultiplikation ist die Funktion

$$\cdot:R^{l\times m}\times R^{m\times n}\to R^{l\times n},\quad (\mathfrak A,\mathfrak B)\mapsto \mathfrak C = \mathfrak A\cdot \mathfrak B\;,$$

wobei die Elemente in $\mathfrak C$ wie folgt definiert sind

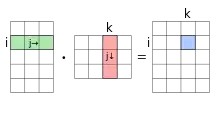
$$c_{ik} = \sum_{j = 1}^ma_{ij}b_{jk}\;.$$

Graphisch passiert folgendes