Skalarmultiplikation

Einfache Sprache

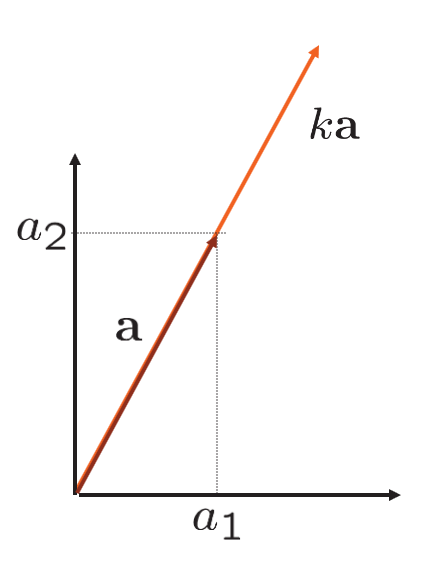
Bei der Skalarmultiplikation wird eine Vektor oder eine Matrix mit einer beliebigen reelle Zahl (auch Skalar genannt) multipliziert, indem komponentenweise die einzelnen Einträge des Vektors bzw. der Matrix mit dem Skalar multipliziert werden.

Def. Skalarmultiplikation mit Vektoren

Sei $c\in\mathbb R$ ein Skalar und $\mathfrak x = \left( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right)$ ein Vektor in $\mathbb R^n$. Dann ist die Skalarmultiplikation definiert durch

$$c\mathfrak x = c\left( \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right)= \left( \begin{array}{c} cx_1 \\ \vdots \\ cx_n \end{array} \right)\;.$$

Def. Skalarmultiplikation mit Vektoren

Sei $c\in\mathbb R$ ein Skalar und $\mathfrak A:n\times m$ eine Matrix in $\mathbb R^n$. Dann ist die Skalarmultiplikation definiert durch

$$\begin{align}c\mathfrak A &= c\left( \begin{array}{cccc} a_{11}& a_{12}&\cdots &a_{1m} \\ a_{21}& a_{22}&\cdots &a_{2m} \\ \vdots \\ a_{n1}& a_{n2}&\cdots &a_{nm} \\ \end{array} \right)\\ &= c\left( \begin{array}{cccc} a_{11}& a_{12}&\cdots &a_{1m} \\ a_{21}& a_{22}&\cdots &a_{2m} \\ \vdots \\ a_{n1}& a_{n2}&\cdots &a_{nm} \\ \end{array} \right)\\\end{align}$$