Point-set registration
Einfache Sprache
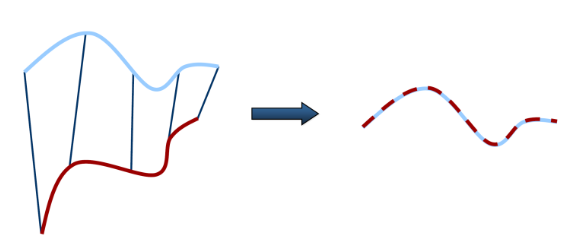
Bei der Point-set registration sind 2 Menge mit korrespondierenden Punkten (Punktwolke) gegeben. Ziel ist es die Funktion zu berechnen, welche mit dem kleinsten Fehler die eine Punktmenge in die andere Punktmenge abbilden kann.
Def. Point-set registration Problem
Sei $X= \{x_1,\ldots, x_M\}$ und $P =\{p_1,\ldots,p_N\}$ Mengen, die aus Punkten in einem Vektorraum $\mathbb R^d$ bestehen, also Punktwolken. Sei $\mathrm{dist}(\cdot,\cdot)$ eine Distanzfunktion, für die Entfernung zweier Punktwolken. Ziel ist es die Abbildungsmatrix $T^*$ zu finden, welche die Distanz zwischen $X$ und $P$ minimiert. Also
$$T^*=\arg\min_{T}\mathrm{dist}(X,T(P))\;.$$
Beispiel
Wenn wir die Abbildungsmatrix $T(\mathfrak x) =\mathfrak{Rx-t}$ aus einer Translation $\mathfrak t$ und einer Rotation $\mathfrak R$ besteht, wir die euklidische Metrik für die Distanz verwenden und die Methode der kleinsten Quadrate anwenden, dann erhalten wir folgende Minimierungsproblem
$$E(\mathfrak{R,t})=\frac{1}N \sum_{i=1}^N||\mathfrak x_i-\mathfrak{Rp}_i-\mathfrak t||_2\;,$$wobei der Punkt $\mathfrak x_i$ der transformierte Punkt $\mathfrak p_i$ ist. Sie stimmen überein.
Bekannte Übereinstimmung
Ist bekannt welche Punkte aus $X$ und $P$ übereinstimmen, so kann die Transformation in geschlossener Form berechnet werden.
 Dazu
Dazu