Erweiterte Kalman-Filter

Einfache Sprache

Der Erweiterte Kalman-Filter berechnet, im Gegensatz zum Kalman-Filter, nicht den exakten normalverteilten Belief, sondern eine normalverteilte Approximation des Beliefs. Es wird die Differenz der Funktionen benötigt!!!!

Def. Erweiterte Kalman-Filter

Der Erweiterte Kalman-Filter ist ein Kalman-Filter bei dem die Annahme der Linearität der Transitionsfunktion und der Linearität der Wahrnehmungsfunktion gelockert werden so, dass auch Nichtlineare Funktion ($g$ und $h$) erlaubt sind. Dadurch ist nach jeder Iteration der Belief $\text{Bel}(\mathfrak x_t)$ nicht mehr normalverteilt. Bei der nächsten Iteration ist dann die zentrale Annahme, das der Belief normalverteilt ist, nicht mehr erfüllt. Daher muss nach der der Anwendung einer Nichtlineare Funktion der Belief linearisiert werden. Konkret ändert sich im Vergleich zum Kalman-Filter die Transitionsfunktion und Wahrnehmungsfunktion
$$\mathfrak x_t=g(\mathfrak u_t,\mathfrak x_{t_1}) +\mathfrak e_t$$
und
$$\mathfrak z_t=h(\mathfrak x_t) +\mathfrak d_t\;.$$

EKF Linearisierung

Idee

Die Nichtlineare Funktion $g$ wird durch eine Taylor-Näherung ersten Grades approximiert. Dafür muss die erste Ableitung, auch Jacobi-Matrix genannt, von $g$ berechnet werden

$$g'(\mathfrak u_t,\mathfrak x_{t_1}) = \frac{\partial g(\mathfrak u_t,\mathfrak x_{t_1})}{\partial\mathfrak x_{t-1}}\;.$$

Da wir mit Normalverteilung annehmen ist der beste Punkt-Schätzung des Zustands der Erwartungswert $\mathfrak m_{t-1}$. Daraus ergibt sich Taylor-Näherung

$$\begin{align}g(\mathfrak u_t,\mathfrak x_{t-1}) &\approx g(\mathfrak u_t,\mathfrak m_{t-1}) + g'(\mathfrak u_t,\mathfrak m_{t-1})(\mathfrak x_{t-1}-\mathfrak m_{t-1}) &\Huge|\normalsize\text{Taylor-Formel}\\&=g(\mathfrak u_t,\mathfrak m_{t-1}) + \mathfrak G_t(\mathfrak x_{t-1}-\mathfrak m_{t-1}) &\Huge|\normalsize\text{Jacobi-Matrix}\\\end{align}$$

Die Jacobi-Matrix $\mathfrak G_t$ ist anhäng vom Zustand und der Aktion, also von der Zeit $t$. Als Zustandsübergangswahrscheinlichkeit ergibt sich

$$p(\mathfrak x_t\mid \mathfrak u_t,\mathfrak x_{t-1})= \text{det}(2\pi\mathfrak R_t)^{-1/2}\text{exp}\left(-\frac{1}{2}\left(\mathfrak x_t-g\left(\mathfrak u_t,\mathfrak m_{t-1}) + \mathfrak G_t(\mathfrak x_{t-1}-\mathfrak m_{t-1}\right) \right)^T\mathfrak R_t^{-1}\left(\mathfrak x_t-g\left(\mathfrak u_t,\mathfrak m_{t-1}) + \mathfrak G_t(\mathfrak x_{t-1}-\mathfrak m_{t-1}\right) \right)\right)$$

Analog ergibt sich für $h$

$$\begin{align}h(\mathfrak x_{t}) &\approx h(\mathfrak {\bar m}_t) + h'(\mathfrak {\bar{m}}_{t})(\mathfrak x_{t}-\mathfrak{\bar m}_{t}) &\Huge|\normalsize\text{Taylor-Formel}\\&= h(\mathfrak {\bar m}_t) + \mathfrak H_t(\mathfrak x_{t}-\mathfrak{\bar m}_{t}) &\Huge|\normalsize\text{Jacobi-Matrix}\\\end{align}$$

Hier wird aber $\mathfrak{\bar m}_t$ genommen anstatt $\mathfrak m_{t-1}$, da das der neue wahrscheinlichste Zustand ist. Als Wahrnehmungswahrscheinlichkeit ergibt sich

$$p(\mathfrak z_t\mid \mathfrak x_t)= \text{det}(2\pi\mathfrak Q_t)^{-1/2}\text{exp}\left(-\frac{1}{2}\left(\mathfrak z_t-h\left(\mathfrak {\bar m}_t) -\mathfrak H_t(\mathfrak x_{t}-\mathfrak{\bar m}_{t}\right) \right)^T\mathfrak Q_t^{-1}\left(\mathfrak z_t-\left(\mathfrak {\bar m}_t) - \mathfrak H_t(\mathfrak x_{t}-\mathfrak{\bar m}_{t}\right) \right)\right)$$

Beispiel

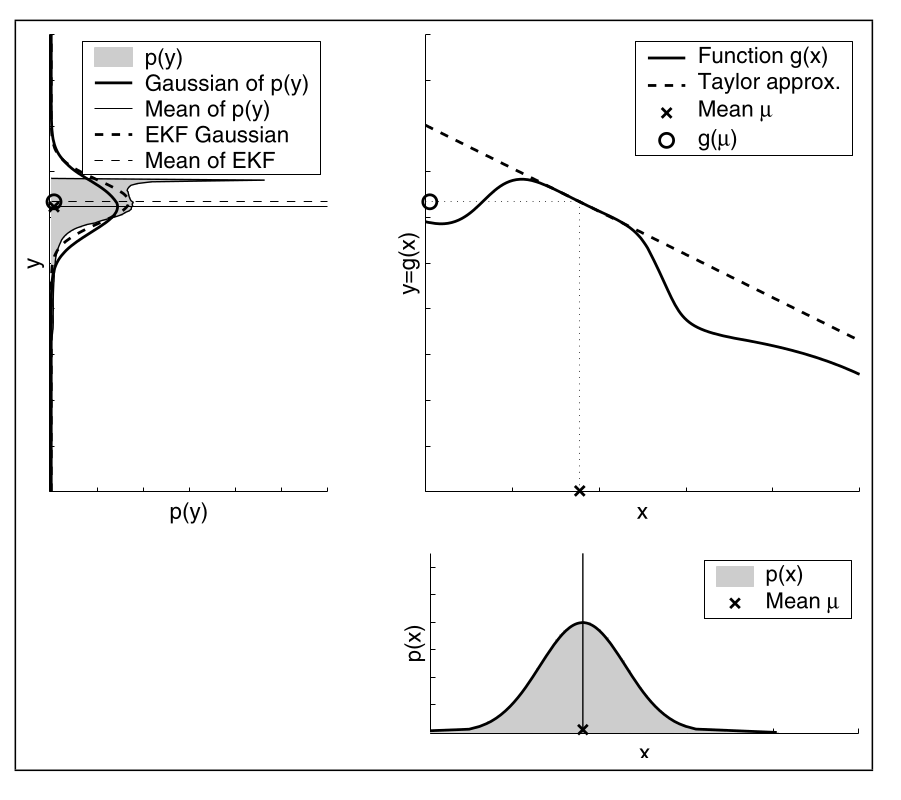
Hier sieht man wie die EKF Linearisierung funktioniert. Es wird zuerst die Taylor-Näherung berechnet. Die daruch erhaltene Tangente (Tylor approx.) wird dann auf die Normalverteilung angewendet und man erhält die neue Normalverteilung. Der Unterschied zwischen der Approximation und der Monte-Carlo Schätzung ist der Fehler der durch die Approximation in Kauf genommen wird. Die Monte-Carlo Schätzung, im Bild links oben die durchgezogenen Linien wird folgender Maßen erhalten: (1) Ziehe 500.000 Zufallszahlen von der Normalverteilung $p(x)$, (2) wende $g$ auf die Zufallszahlen an und berechne den Mittelwert und die Varianz von der transformierten Zufallszahlen.

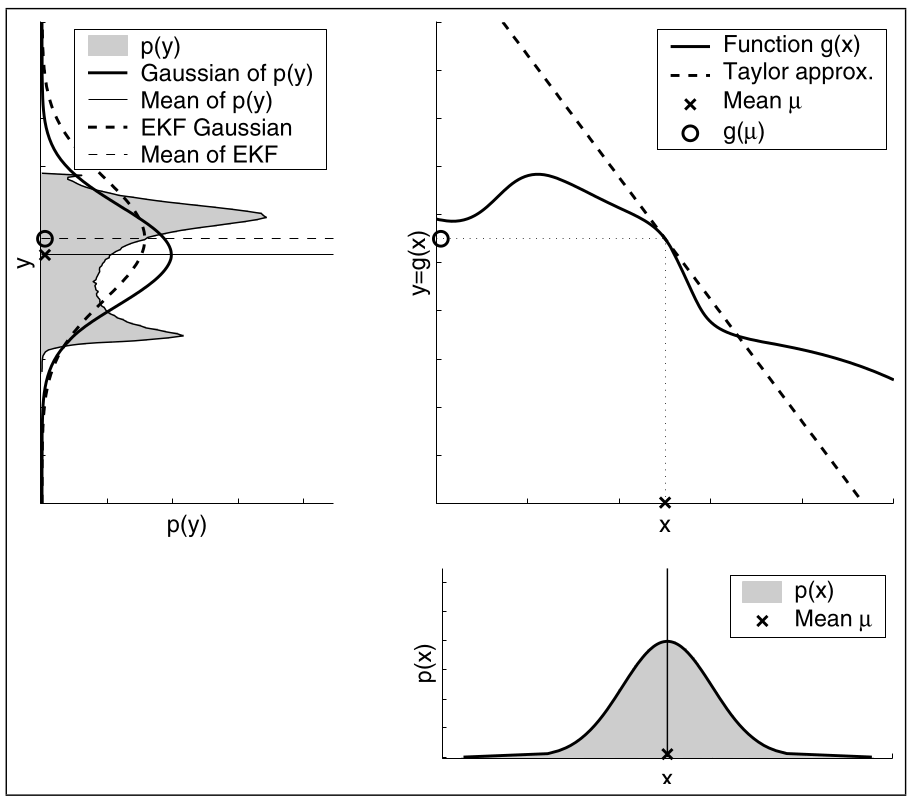
Erweiterte Kalman-Filter Linearisierung 1.png

Bewertung

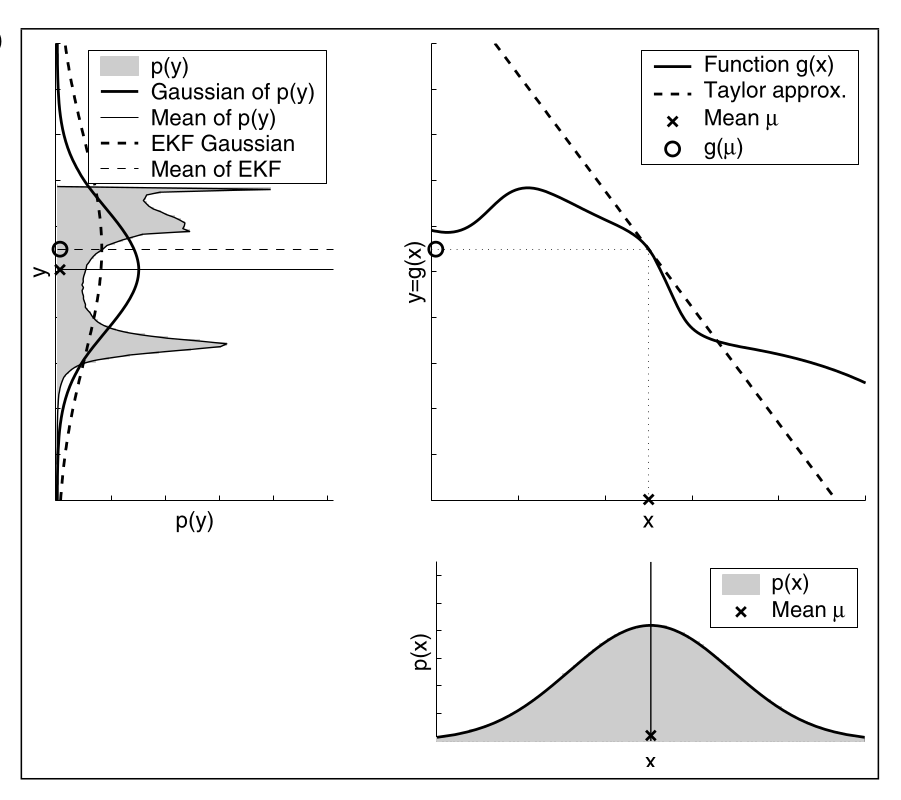
Die Güte der EKF Linearisierung hängt maßgeblich von zwei Faktoren ab:

der Grad der Ungewissheit des Beliefs und
der Grad an Nichtlinearität der zu approbierenden Transformationsfunktion.

Ungewissheit

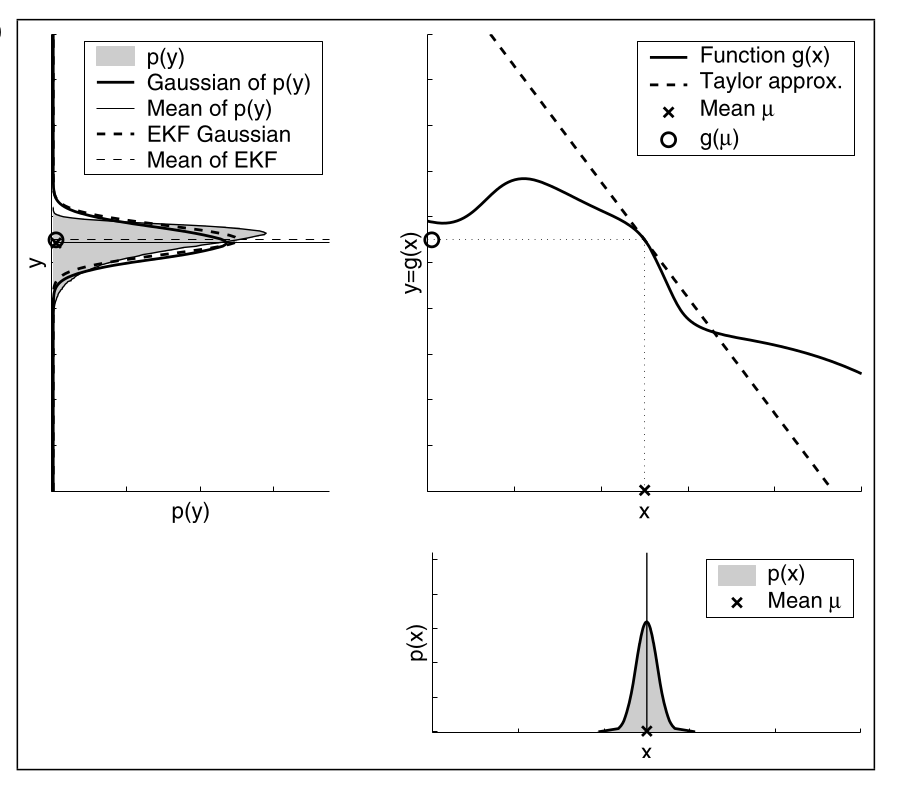
Hier ist die Approximation nicht gut, da die Ungewissheit von $p(x)$ zu hoch ist. Erweiterte Kalman-Filter Linearisierung 2.png Hier ist die Approximation gut, da die Ungewissheit von $p(x)$ gering ist.

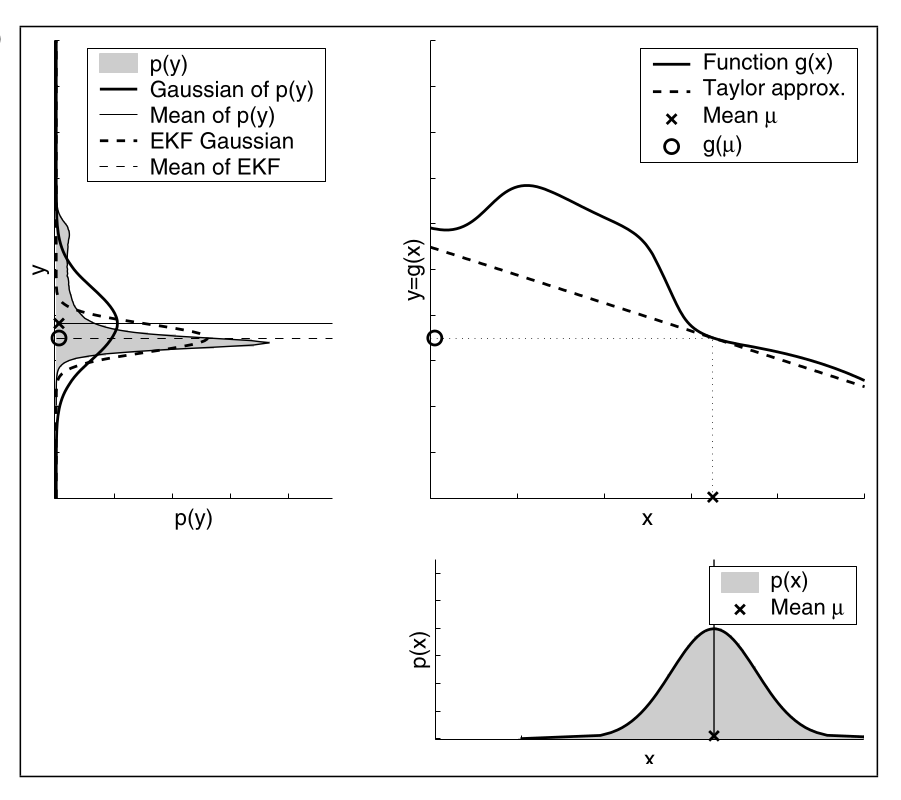
Nichtlinearität

Hier ist die Approximation nicht gut, da die Funktion $g(x)$ an der stelle $\mu$ sehr nichtlinear ist.
Erweiterte Kalman-Filter Linearisierung 4.png Hier ist die Approximation gut, da die Funktion $g(x)$ an der stelle $\mu$ sehr linear ist.

Siehe auch Vergleich EKF und UKF

Algorithmus

In Vektor-Schreibweise wird eine Iteration des EKF durch folgenden Algorithmus berechnet:

	\begin{algorithm}
	\caption{Vektorisierter Erweiterte Kalman-Filter}
	\begin{algorithmic}
	\Input Mittelwertvektor $\mathfrak m_{t-1}$, Kovarianzmatrix $\mathfrak S_{t-1}$, Beobachtungsvektor $\mathfrak z_t$, Transitionsvektor $\mathfrak u_t$
	\Procedure{vectorized-EFK}{$\mathfrak m_{t-1},\mathfrak S_{t-1}, \mathfrak z_t, \mathfrak u_t$}
	\State $\bar\mathfrak m_t \gets g(\mathfrak u_t, \mathfrak m_{t-1})$\Comment{Transformation.}
	\State $\bar\mathfrak S_t \gets \mathfrak G_t\mathfrak S_{t-1}\mathfrak G_t^T+ \mathfrak R_t$
	\State $\mathfrak K_t \gets \bar\mathfrak S_t\mathfrak C_{t}^T\left(\mathfrak C_t\bar\mathfrak S_t\mathfrak C^T_t+\mathfrak Q_t\right)^{-1}$\Comment{kalman gain.}
	\State $\mathfrak m_t \gets \bar\mathfrak m_t + \mathfrak K_t\left(\mathfrak z_t - h(\bar\mathfrak m_t)\right)$\Comment{Messung.}
	\State $\mathfrak S_t \gets \left(\mathfrak I - \mathfrak K_t\mathfrak H_t \right)\bar\mathfrak S_t$
	\Return $\mathfrak m_t,\mathfrak S_t$
    \EndProcedure
	\end{algorithmic}
	\end{algorithm}

Laufzeit durch $\mathcal O(n^2+k^{2.4})$ begrenzt.

Home: