inverses Belegungsgitterkartensensormodell

Einfache Sprache

Das inverses Belegungsgitterkartensensormodell ermöglich es geben eine Zustand und eine Wahrnehmung für eine Zelle einer Belegungsgitterkarte die Belegwahrscheinlichkeit zu berechnen.

Sonar

Für die Belegungsgitterkartierung und einen Sonar ist das inverses Belegungsgitterkartensensormodell als Algorithmus wie folgt definiert:

\begin{algorithm}
\caption{inverses Belegungsgitterkartensensormodell}
\begin{algorithmic}
\Input Zelle $m_i$, Wahrnehmung $z_t$, Roboterpose $x_t$
\Procedure{inverse-range-sensor-model}{$m_i,x_t,z_t$}
	\State Let $x_i,y_i$ be the center (of mass) of $m_i$
	\State $r \gets \sqrt{(x_i-x)^2+(y_i-y)2}$
	\State $\phi \gets \mathrm{atan2}(y_i-y,x_i-x)-\theta$
	\State $k \gets \argmin_j\left|\phi-\theta_{j,\mathrm{sens}}\right|$
	\If{$r > \min(z_\mathrm{max}, z_t^k+\alpha/2)$ or $\left|\phi-\theta_{k,\mathrm{sens}}\right|>\beta/2$}
		\Return $l_0$
	\Elif{$z_t^k < z_\mathrm{max}$ and $|r-z_t^k|<\alpha/2$}
		\Return $l_\mathrm{occ}$
	\Else
		
		\Return $l_\mathrm{free}$
    \EndIf
\EndProcedure
\end{algorithmic}
\end{algorithm}

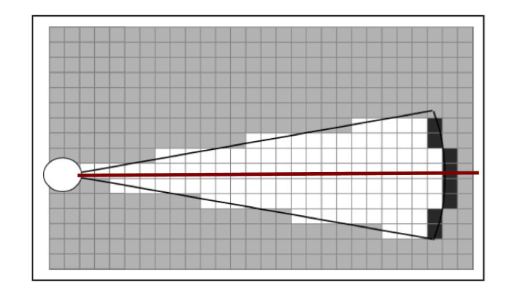
Beispiel

Je dunkler desto hoher ist die Belegwahrscheinlichkeit.