Unscented Kalman-Filter

Einfache Sprache

Der Unscented Kalman-Filter baut auf dem Kalman-Filter auf erlaubt aber Nichtlineare Funktion. Dabei werden diese stochastisch linearisiert durch eine gewichtete Lineare Regression.

Unscented Transformation

Vereinfacht

Die Linearisierung durch Unscented Transformation funktioniert vereinfacht wie folgt:

Es werden sogenannte Sigma-Punkte von dem normalverteilten Belief deterministisch ausgewählt.
Für jeden Punkt wird eine Gewicht für die Mittelwert-Berechnung und die Kovarianz-Berechnung ermittelt.
Auf die Sigma-Punkte wird die Nichtlineare Funktion angewendet.
Die gewichteten Summen der transformierten Sigma-Punkten ist dann der neue Belief.

Generell

Die Sigma-Punkte $\mathcal X^{[i]}$ sind der Mittelwert und symmetrisch entlang der Hauptachsen der Kovarianz. Für einen $n$-Dimensionale multivariate Normalverteilung hat man also $2n+1$ Sigma-Punkte die wie folgt definiert sind

$$\mathcal X^{[0]}= \mathfrak m$$

$$\mathcal X^{[i]}= \mathfrak m+\left(\sqrt{(n+\lambda)\mathfrak S}\right)_i\quad \forall i\in \{1,\ldots,n\}$$

$$\mathcal X^{[i]}= \mathfrak m-\left(\sqrt{(n+\lambda)\mathfrak S}\right)_{i-n}\quad \forall i\in \{n+1,\ldots,2n\}$$

wobei $\lambda = \alpha^2(n+\kappa) -n$, mit $\alpha$ und $\kappa$ entscheidet für die Entfernung der Sigma-Punkte vom Mittelwert.

Die zwei gewichte für den jeweiligen Sigma-Punkt, $w_m^{[i]}$ für denn Mittelwert und $w_c^{[i]}$ für die Kovarianz, werde wie folgt berechnet

$$w_m^{[0]} = \frac{\lambda}{n+\lambda}$$$$w_c^{[0]} = \frac{\lambda}{n+\lambda}+(1+\alpha^2+\beta)$$

$$w_m^{[i]} = w_c^{[i]} = \frac{1}{2(n+\lambda)}$$

wobei $\beta$ abhängig von der tatsächlichen Verteilung des Beliefs gewählt werden sollte. Ist der Belief perfekt normalverteilt, dann ist $\beta=2$ optimal.

Dann werden die Funktion $g$ auf die Sigma-Punkte $\mathcal X^{[i]}$ angewendet und es ergibt sich $\mathcal Y^{[i]}$.

$$\mathcal Y^{[i]}= g\left(\mathcal X^{[i]}\right)$$

Die Parameter des resultierenden Beliefs werden dann als gewichtete Summe von $\mathcal Y^{[i]}$ berechnet:

$$\mathfrak m' = \sum_{i=0}^{2n}w_m^{[i]}\mathcal Y^{[i]}$$

$$\mathfrak m' = \sum_{i=0}^{2n}w_c^{[i]}(\mathcal Y^{[i]}-\mathfrak m')(\mathcal Y^{[i]}-\mathfrak m')^T$$

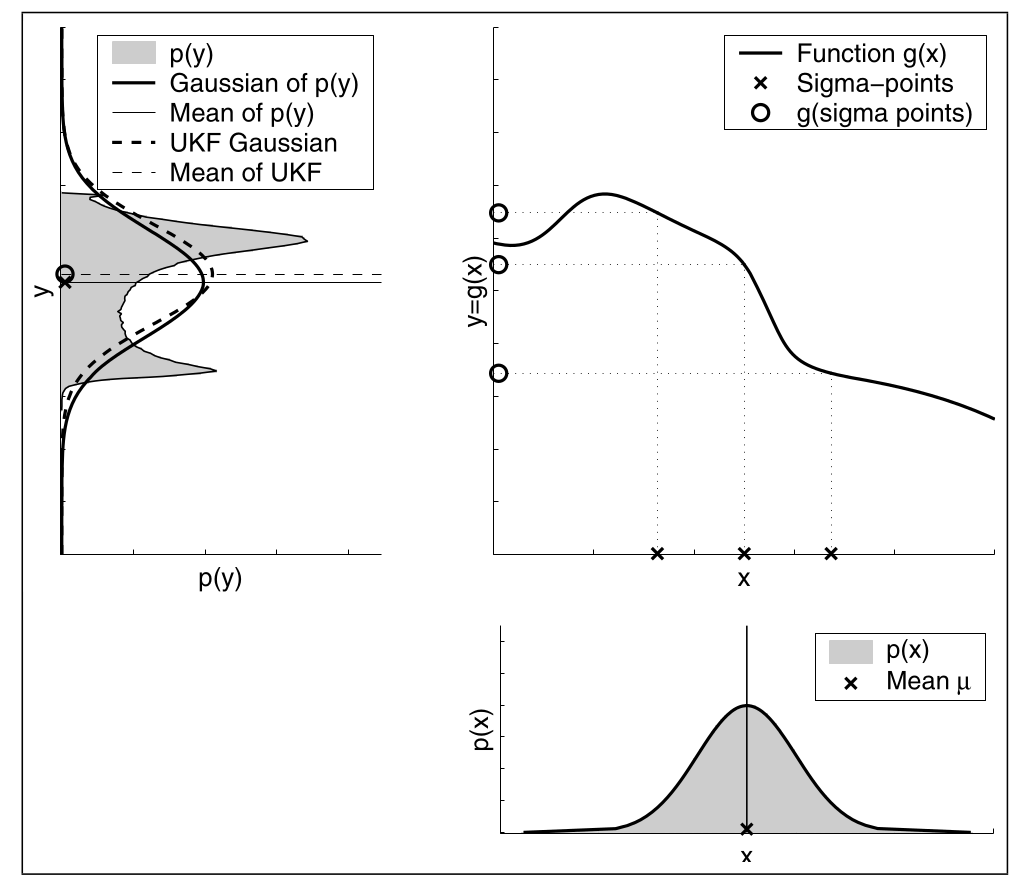
Beispiel

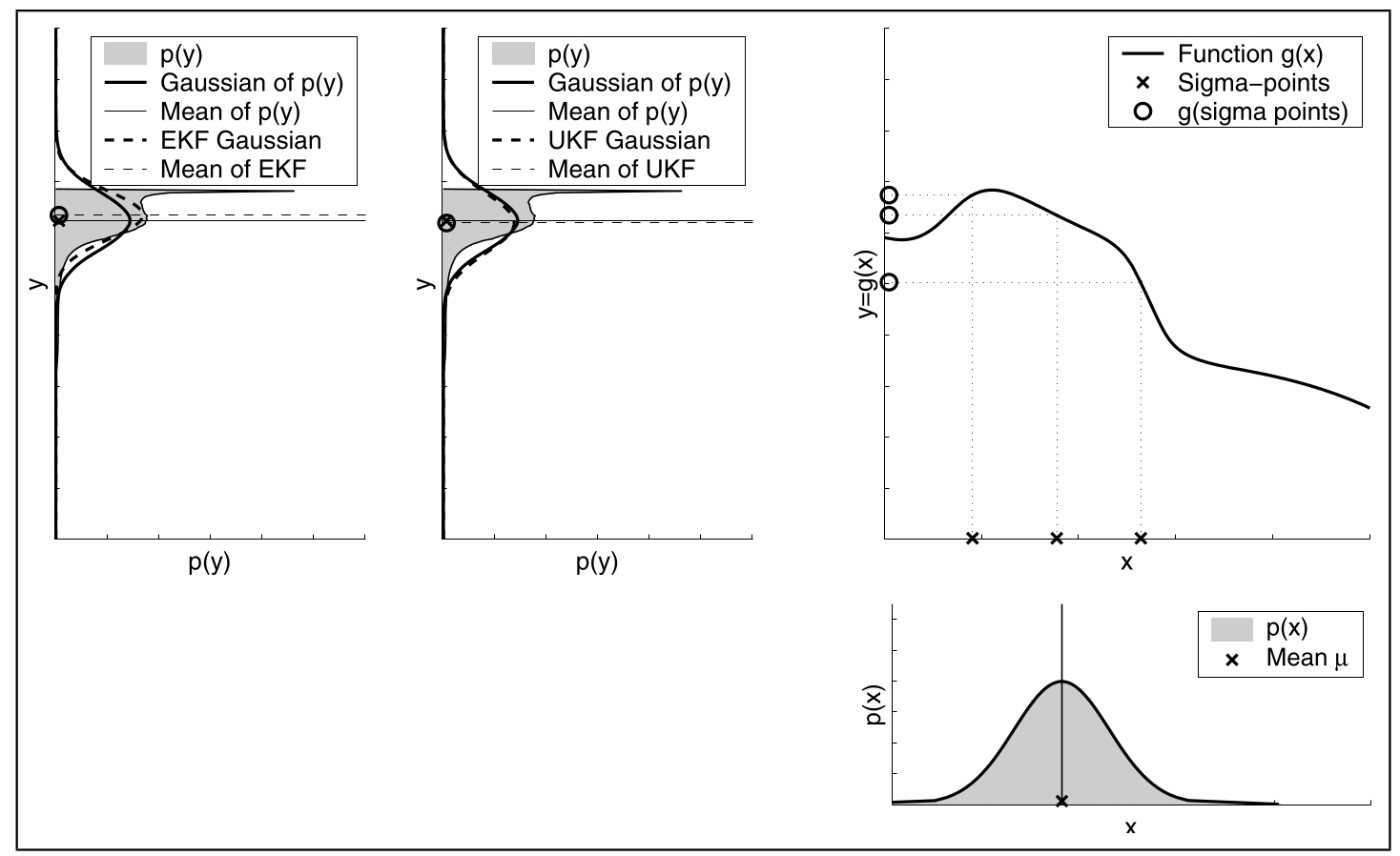
Hier sieht man UKF Transformation im 1-Dimensionalen Raum. Daher gibt es $2\cdot1 +1=3$ Sigma-Punkte. Unscented Kalman-Filter 1.png

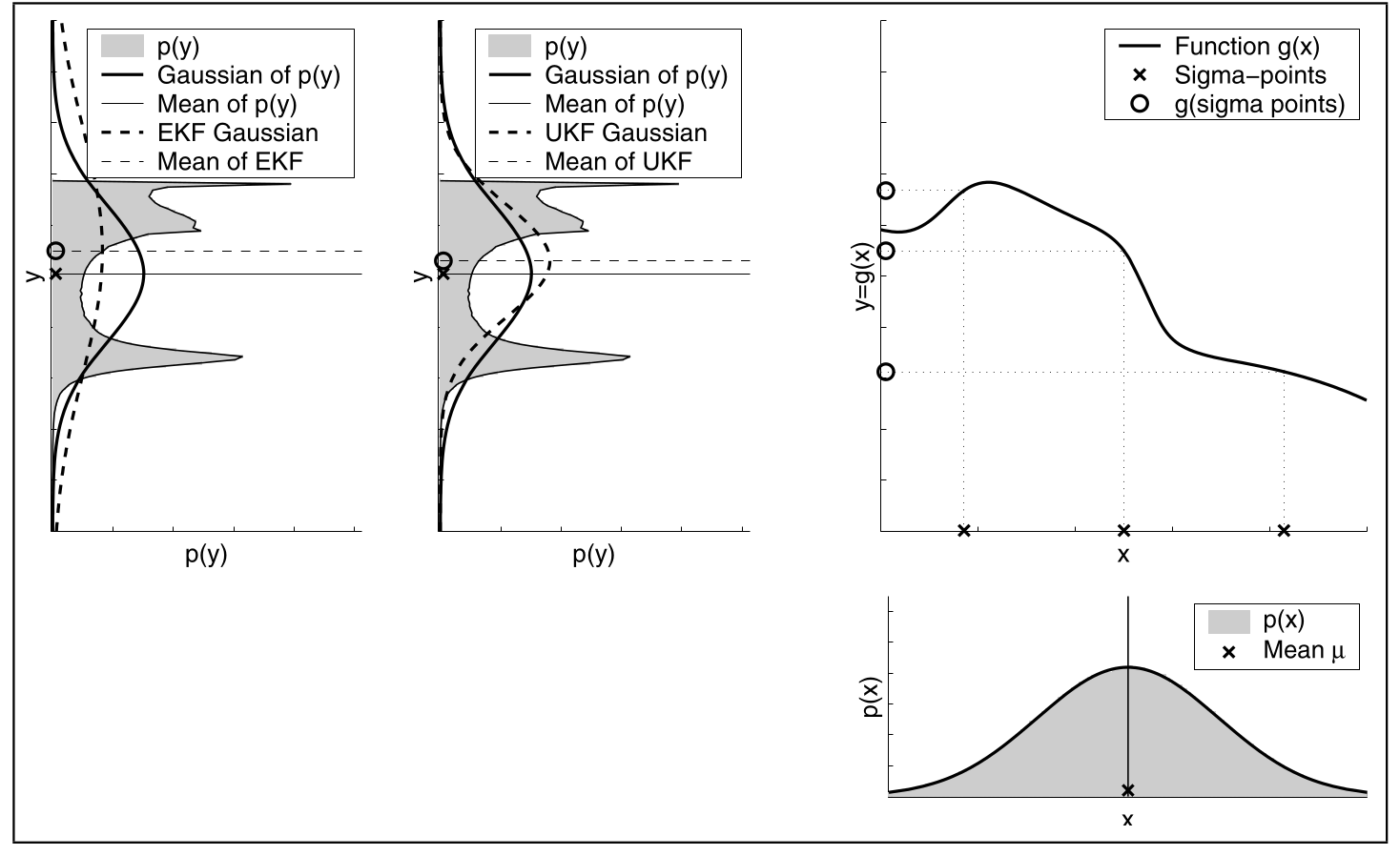
Vergleich EKF und UKF

Es wird EKF und UKF verglichen.

Unsicherheit

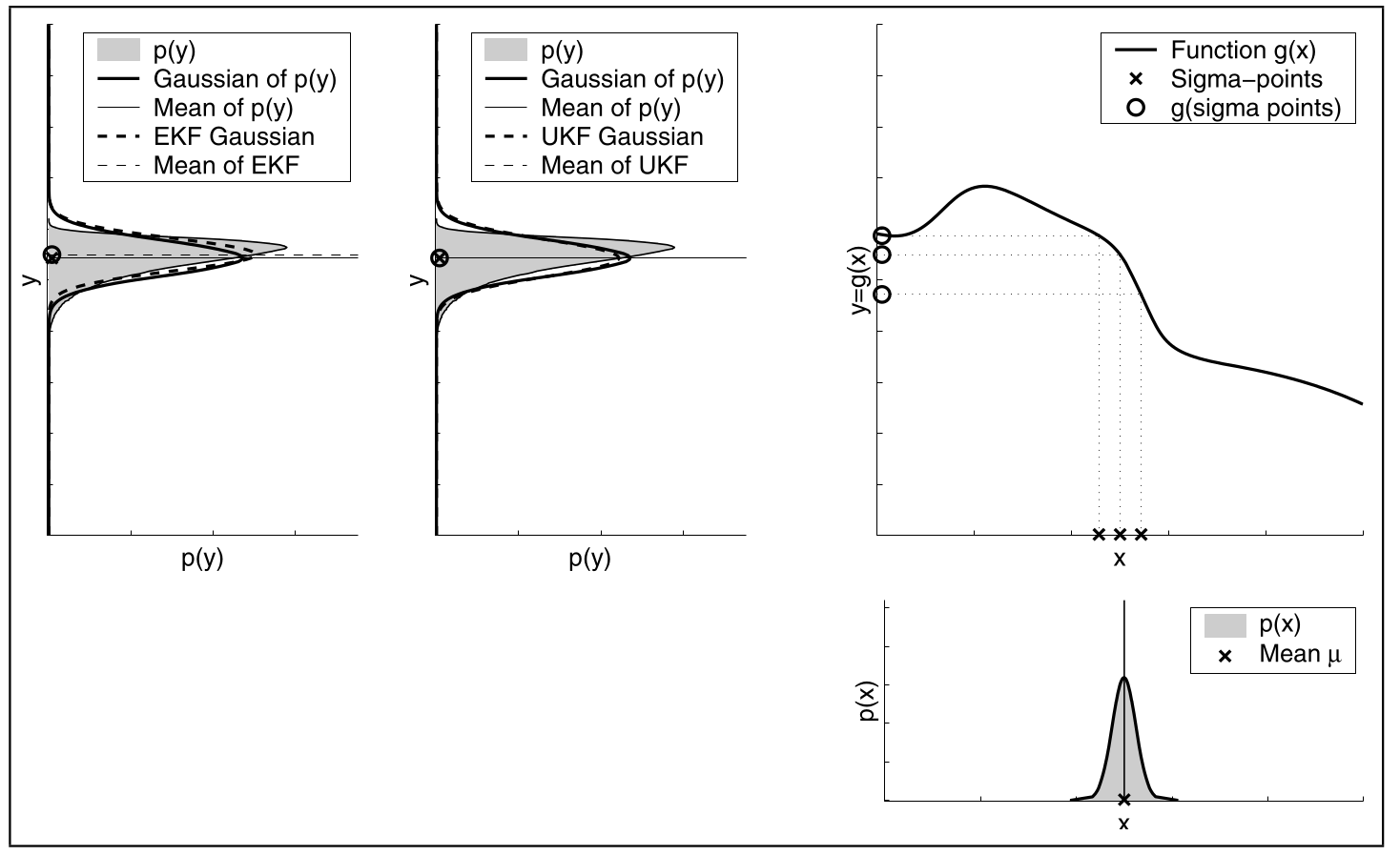
Hier sieht man, dass UKF besser mit hoher Ungewissheit des Beliefs umgeht. Unscented Kalman-Filter 2.png Hier sieht man das bei geringer Ungewissheit der Approximationsfehler kleiner wird. Unscented Kalman-Filter 3.png

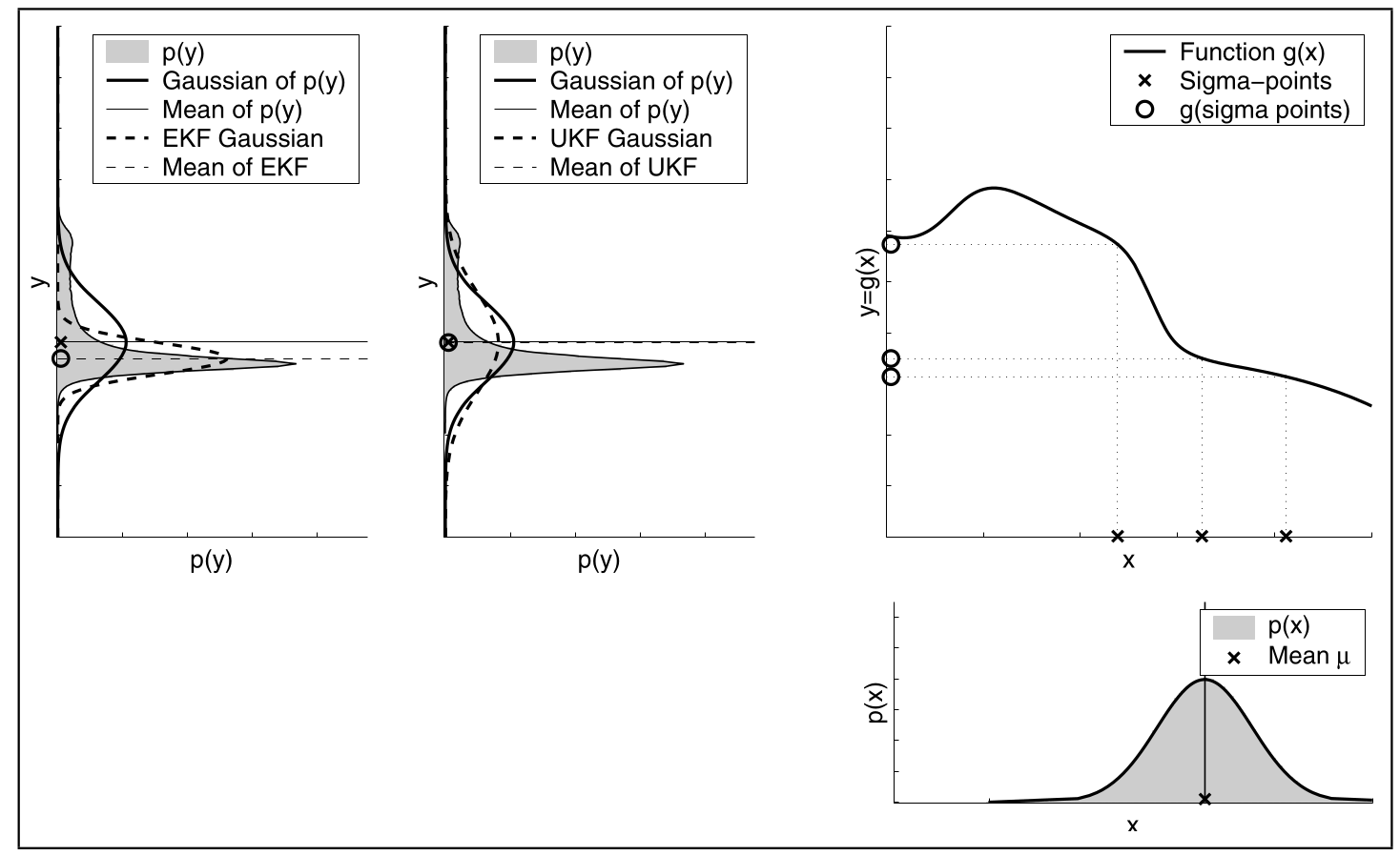
Nichtlinearität

Hier sieht man das UKF besser mit hoher Nichtlinearität umgehen kann als EKF Unscented Kalman-Filter 4.png Hier sieht man das UKF auch bei lineareren Funktionen besser ist. Unscented Kalman-Filter 5.png

Algorithmus

In Vektor-Schreibweise wird eine Iteration des UKF durch folgenden Algorithmus berechnet:

	\begin{algorithm}
	\caption{Vektorisierter Unscented Kalman-Filter}
	\begin{algorithmic}
	\Input Mittelwertvektor $\mathfrak m_{t-1}$, Kovarianzmatrix $\mathfrak S_{t-1}$, Beobachtungsvektor $\mathfrak z_t$, Transitionsvektor $\mathfrak u_t$
	\Procedure{vectorized-UFK}{$\mathfrak m_{t-1},\mathfrak S_{t-1}, \mathfrak z_t, \mathfrak u_t$}
	\State $\gamma \gets \sqrt{n+\lambda}$ 
	\State $\mathcal X_{t-1} \gets \left( \begin{array}{ccc} \mathfrak m_{t-1} & \mathfrak m_{t-1}+\gamma\sqrt{\mathfrak S_{t-1}} & \mathfrak m_{t-1}-\gamma\sqrt{\mathfrak S_{t-1}}\end{array} \right)$
	\State $\mathcal {\bar X}^*_t \gets g(\mathfrak u_t,\mathcal X_{t-1})$
	\State $\bar\mathfrak m_t \gets \sum_{i = 0}^{2n}w_m^{[i]}{\mathcal{\bar X}_t^*}^{[i]}$

	\State $\bar\mathfrak S_t \gets \sum_{i = 0}^{2n}w_c^{[i]}\left({\mathcal{\bar X}_t^*}^{[i]}-\mathfrak{\bar m}_t\right)\left({\mathcal{\bar X}_t^*}^{[i]}-\mathfrak{\bar m}_t\right)^T+ \mathfrak R_t$
		\State $\mathcal {\bar X}_{t} \gets \left( \begin{array}{ccc} \mathfrak {\bar m}_{t} & \mathfrak {\bar m}_{t}+\gamma\sqrt{\mathfrak {\bar S}_{t}} & \mathfrak {\bar m}_{t}-\gamma\sqrt{\mathfrak {\bar S}_{t}}\end{array} \right)$

	\State $\mathcal{\bar Z}_t = h(\mathcal {\bar X}_t)$
	\State $\mathcal{\bar z}_t = \gets \sum_{i = 0}^{2n}w_m^{[i]}{\mathcal{\bar Z}_t}^{[i]}$
	
	\State $\mathcal S_t \gets \sum_{i = 0}^{2n}w_c^{[i]}\left({\mathcal{\bar Z}_t}^{[i]}-\mathfrak{\bar z}_t\right)\left({\mathcal{\bar Z}_t}^{[i]}-\mathfrak{\bar z}_t\right)^T+ \mathfrak Q_t$
	
	\State $\mathfrak {\bar S}_t^{x,z} \gets \sum_{i = 0}^{2n}w_c^{[i]}\left({\mathcal{\bar X}_t}^{[i]}-\mathfrak{\bar m}_t\right)\left({\mathcal{\bar Z}_t}^{[i]}-\mathfrak{\bar z}_t\right)^T$
	
	
	\State $\mathfrak K_t \gets \mathfrak {\bar S}_t^{x,z}\mathcal S_t^{-1}$
	\State $\mathfrak m_t \gets \bar\mathfrak m_t + \mathfrak K_t\left(\mathfrak z_t - \bar\mathfrak z_t\right)$ \Comment{Messung.}
	\State $\mathfrak S_t \gets \bar\mathfrak S_t - \mathfrak K_t \mathcal S_t \mathfrak K_t^T$
	\Return $\mathfrak m_t,\mathfrak S_t$
    \EndProcedure
	\end{algorithmic}
	\end{algorithm}

Laufzeit durch $\mathcal O(n^2+k^{2.4})$ begrenzt.

Home: