Koppelnavigation

Einfache Sprache

Die Koppelnavigation ist die Ortsbestimmung anhand der Bewegungsrichtung und Geschwindigkeit. Da die Aktion noch nicht ausgeführt werden sein muss, wird das Verfahren für Roboterplannung verwendet.

Def. Koppelnavigation

Begriffe (im 2D-Raum)

Die in der Wahrscheinlichkeitstheoretische Robotik verwendeten Begriffe werden bei der Koppelnavigation wie folgt definiert:

Die Aktion $u_t$ ist ein Vektor der sich aus der Translationsgeschwindigkeit $v_t$ und der Rotationsgeschwindigkeit $w_t$ zusammen setzt. Also $$u_t = \left( \begin{array}{c} v_t\\ w_t\end{array} \right)\;.$$
Der Zustand des Roboters ist die Roboterpose im 2D-Raum. Dabei gibt es den aktuellen Zustand $$\mathfrak x_{t-1} = \left( \begin{array}{c} x\\ y\\ \theta \end{array} \right)$$ und den hypothetischen Nachfolgezustand $$\mathfrak x_t = \left( \begin{array}{c} x'\\ y'\\ \theta' \end{array} \right)\;.$$
Die Ausgabe des Koppelnavigationsalgorithmus ist die Wahrscheinlichkeit das wir ausgehen von $x_{t-1}$ bei Aktion $u_t$ über einen festen Zeitraum $\Delta t$ uns bei $x_t$ befinden. Also $$p(x_t\mid x_{t-1},u_t)\;.$$
Die Parameter $\alpha_1,\ldots,\alpha_6$ sind Roboter spezifisch.

Berechnung in geschlossener Form

Hier sind $u_t, x_{t-1}$ und $x_{t}$ gegeben. Es soll die Wahrscheinlichkeit berechnend werden, das $x_t$ von $x_{t-1}$ mit $u_t$ erreicht wird.

\begin{algorithm}
\caption{Koppelnavigation geschlosse Form}
\begin{algorithmic}
\Input initial pose $x_t$, action $u_t$, hypothesized pose $x_{t-1}$
\Procedure{motion-model-velocity}{$x_t,u_t,x_{t-1}$}
\State $\mu \gets \frac{1}{2}\frac{(x-x')\cos\theta + (y-y')sin\theta}{(y-y')cos\theta+(x-x')\sin\theta}$
\State $x^* \gets \frac{x+x'}{2}+\mu(y-y')$
\State $y^* \gets \frac{y+y'}{2}+\mu(x-x')$
\State $r^* \gets \sqrt{(x-x^*)^2 + (y-y^*)^2}$
\State $\Delta\theta \gets \text{atan2}(y'-y^*,x'-x^*) - \text{atan2}(y-y^*,x-x^*)$
\State $\hat v \gets \frac{\Delta\theta}{\Delta t}r^*$
\State $\hat w \gets \frac{\Delta\theta}{\Delta t}$
\State $\hat \gamma \gets \frac{\theta'-\theta}{\Delta t}-\hat w$
\return \Call{prop}{$v-\hat v, \alpha_1 v^2+\alpha_2 w^2$}$\cdot$ \Call{prop}{$w-\hat w, \alpha_3 v^2+\alpha_4 w^2$}$\cdot$ \Call{prop}{$\hat\gamma, \alpha_5 v^2+\alpha_6 w^2$}
\EndProcedure
\Procedure{prop-normal-distribution}{$q,\sigma$}
\Return $\frac{1}{\sqrt{2\pi \sigma}}\exp\left(-\frac{1 q}{2\sigma}\right)$
\EndProcedure
\Procedure{prop-triangle-distribution}{$a,b$}
\Return $\max\left\{0, \frac{1}{b\sqrt{6}} - \frac{|a|}{6b}\right\}$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Die beiden Funktionen $\text{prop-normal-distribution}$ und $\text{prop-triangle-distribution}$ bekommen einen einen Punkt $q$ bzw. $a$ und eine Standardabweichung $\sigma$ bzw. $b$. Die Rückgabe ist dann die Wahrscheinlichkeit mit der Punkt $q$ von der Normalverteilung $\mathcal N(0,\sigma)$ bzw. von der Dreiecksverteilung stammt.

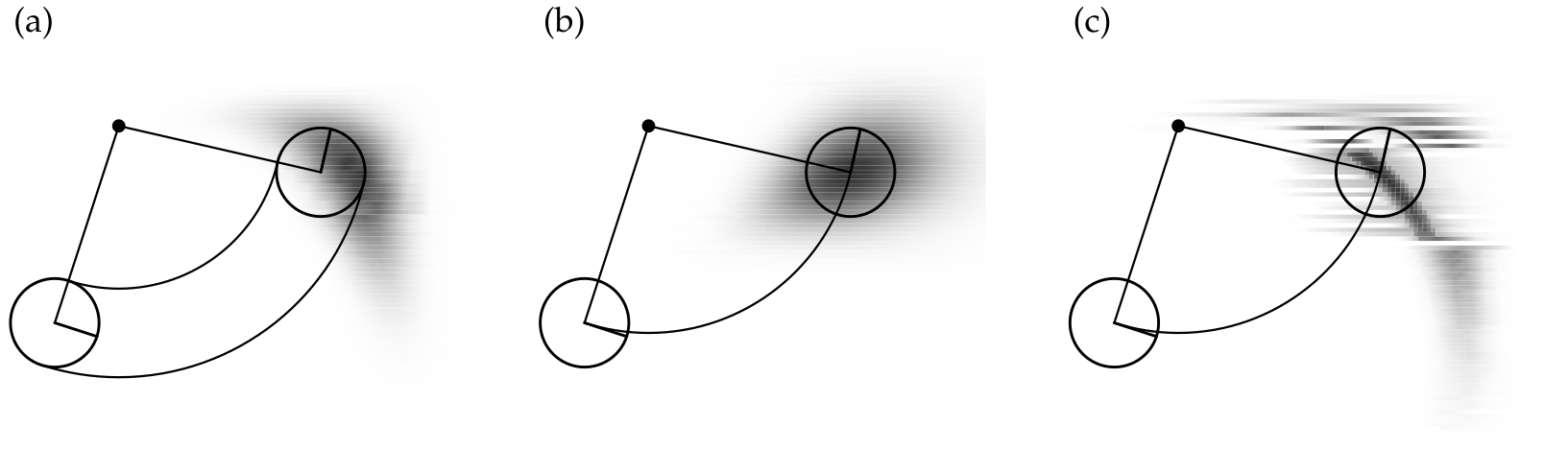
Hier sehen wir ein Beispiel für die Verteilung die durch eine Bewegung entsteht. Die Graustufen beschreiben wie Wahrscheinlich ein Punkt ist. Das wird dadurch ausgerechnet das für alle möglichen Punkte die Wahrscheinlichkeit berechnet wird.

Sampling

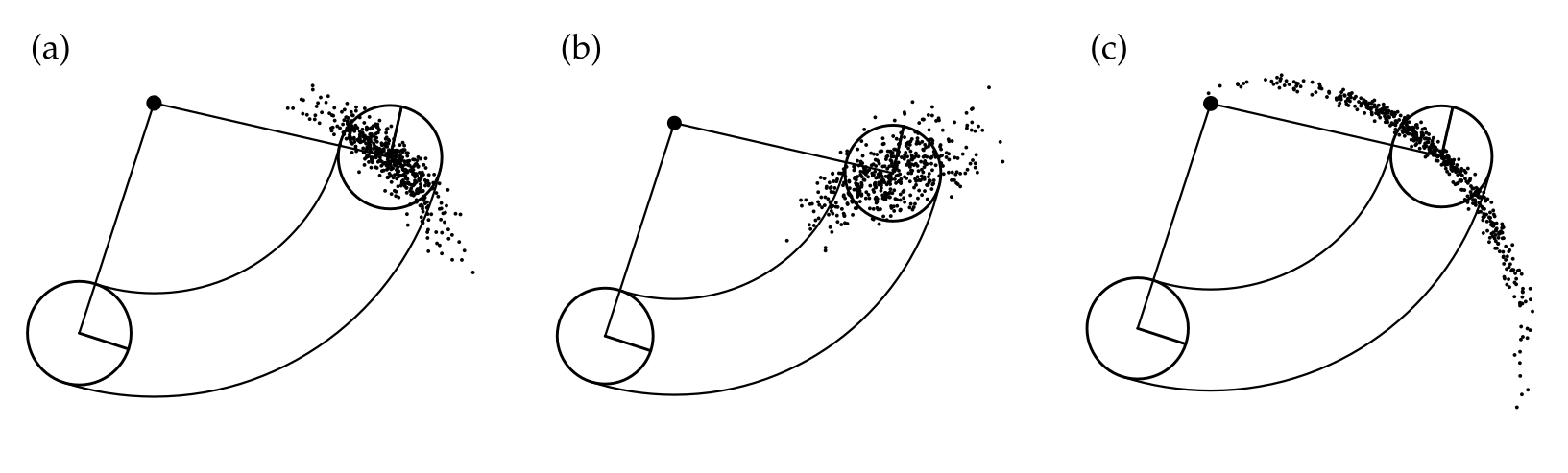
Sei $x_{t-1}$ und $u_t$ bekannt. Bei manchen Methoden (z.B. particle filter) reicht es von der Verteilung $p(x_t\mid x_{t-1}, u_t)$ eine Stichprobe zu ziehen. Es werden also nur wahrscheinliche Kandidaten für $x_t$ zurückgegeben.

\begin{algorithm}
\caption{Koppelnavigation sampling}
\begin{algorithmic}
\Input initial pose $x_{t-1}= \left(x\quad y\quad \theta\right)^T$, action $u_t$
\Procedure{sample-motion-model-velocity}{$x_{t-1},u_t$}
\State $\hat v \gets v +$ \Call{sample}{$\alpha_1v^2 + \alpha_2w^2$}
\State $\hat w \gets w + $ \Call{sample}{$\alpha_3 v^2+\alpha_4 w^2$} 
\State $\hat \gamma \gets $ \Call{sample}{$\alpha_5 v^2+\alpha_6 w^2$}
\State $x' \gets x + \frac{\hat v}{\hat w}(\sin(\theta + \hat w \Delta t) -\sin\theta)
$\State $y' \gets y + \frac{\hat v}{\hat w}(-\sin(\theta + \hat w \Delta t) +\sin\theta)$
\State $\theta' \gets \theta + \hat w\Delta t + \hat\gamma\Delta t$
\Return $x_t = (x'\; y'\; \theta')^T$
\EndProcedure
\Procedure{sample-normal-distribution}{$\sigma$}
\Return $\frac{1}{2}\sum_{i=1}^{12}\textrm{rand}(-\sigma,\sigma)$
\EndProcedure
\Procedure{sample-triangle-distribution}{$b$}
\Return $\frac{\sqrt{6}}{2}(\textrm{rand}(-\sqrt{b},\sqrt{b})+ \textrm{rand}(-\sqrt{b},\sqrt{b}))$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Hier geben die beiden Funktionen sample* eine Zufallszahl die der der Normalverteilung $\mathcal N(0,\sigma)$ bzw. Dreiecksverteilung folgt.

Hier sehen wir eine paar beispiele für 500 Samples und verschiedene Alphawerte.

Home: