Odometrisches Bewegungsmodell

Einfache Sprache

Das Odometrisches Bewegungsmodell nutzt Informationen über die Positionsänderungen des Roboters (odometrische Information). Diese werden meist aus wheel encoder integriert und ist als relative Positionsänderung in einer bestimmten Zeitspanne zu verstehen. Es wird also eine relative Positionsänderung genutzt. Relativ in dem Aspekt das wir nur wissen wie sich der Roboter (vermeintlich) bewegt hat aber nicht die genau Start- und Endposition Da die odometrischen Daten erst anfallen wenn eine Bewegung vollendet wurde, hilft das Verfahren nicht bei der Roboterplannung aber für die Roboterlokalisation.

Begriffe

Technisch gesehen sind odometrische Information Messungen. Vereinfachend wird aber angenommen das es eine Aktion ist. So wird die Dimensionalität reduziert.

Der korrekte Zustand $x_t$ sei als

definiert.

Die Aktion $u_t$ beinhaltet die relative Startpose $\bar x_{t-1}=\left( \begin{array}{ccc} \bar x&\bar y &\bar \theta \end{array} \right)^T$, und relative Endpose $\bar x_{t}=\left( \begin{array}{ccc} \bar x'&\bar y' &\bar \theta' \end{array} \right)^T$, und ist definiert als

Der Balken kennzeichnet Informationen die bezüglich der Roboterpose sind, im Gegensatz zu dem globalen Koordinatensystem.

Idee

Die Kernidee des Odometrisches Bewegungsmodells ist, dass die relative Differenz zwischen $\bar x_{t-1}$ und $\bar x_t$ eine gute Approximation für die tatsächliche Differenz zwischen $x_{t-1}$ und $x_t$.

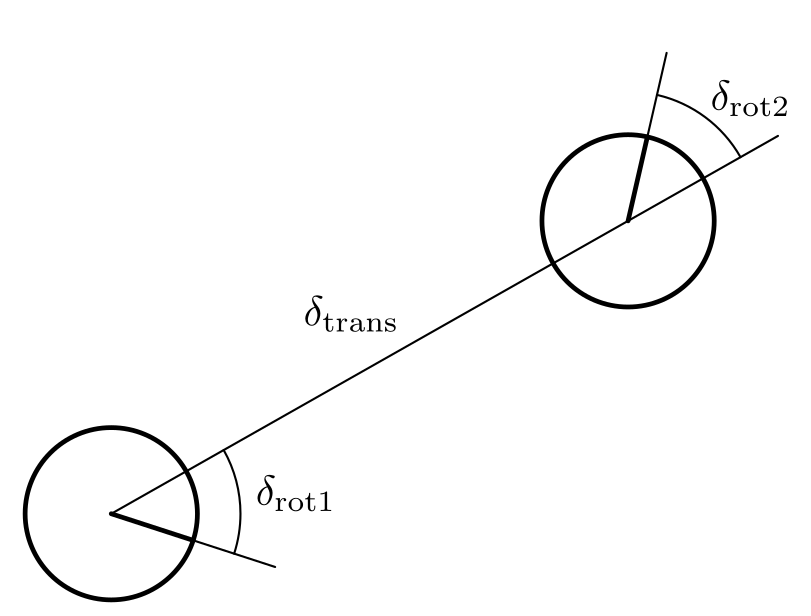
$u_t$ wird, wie im Bild dadrunter, in folgende drei Schritte zerlegt:

1. eine Rotation $\delta_{\textrm{rot}1}$,
2. eine gerade Bewegung $\delta_{\textrm{trans}}$ und
3. eine Rotation $\delta_{\textrm{rot}2}$.

Berechnung in geschlossener Form

Hier sind $x_{t-1}$, $u_t$ und eine hypothetische tatsächliche Endpose $x_t$ gegeben. Folgender Algorithmus berechnet die Wahrscheinlichkeit $p(x_t\mid u_t,x_{t-1})$.

\begin{algorithm}
\caption{Odometrisches Bewegungsmodell geschlosse Form}
\begin{algorithmic}
\Input initial pose $x_t$, action $u_t$, hypothesized pose $x_{t-1}$
\Procedure{motion-model-odometry}{$x_t,u_t,x_{t-1}$}

\State $\delta_{\textrm{rot1}} \gets \textrm{atan2}(\bar y'-\bar y, \bar x'-\bar x)-\bar \theta$
\State $\delta_{\textrm{trans}} \gets \sqrt{(\bar x-\bar x')^2+(\bar y-\bar y')^2}$
\State $\delta_{\textrm{rot2}} \gets \bar\theta'-\bar\theta-\delta_{\textrm{rot1}}$

\State $\hat\delta_{\textrm{rot1}} \gets \textrm{atan2}( y'- y,  x'- x)- \theta$
\State $\hat\delta_{\textrm{trans}} \gets \sqrt{(x- x')^2+( y- y')^2}$
\State $\hat\delta_{\textrm{rot2}} \gets \theta'-\theta-\hat\delta_{\textrm{rot1}}$

\State $p_1 \gets$ \Call{prop}{$\delta_{\textrm{rot1}}- \hat\delta_{\textrm{rot1}}, \alpha_1 \hat\delta_{\textrm{rot1}}^2+\alpha_2 \hat\delta_{\textrm{trans}}^2$}

\State $p_2 \gets$ \Call{prop}{$\delta_{\textrm{trans}}- \hat\delta_{\textrm{trans}}, \alpha_3 \hat\delta_{\textrm{trans}}^2+ \alpha_4 (\hat\delta_{\textrm{rot1}}^2  \hat\delta_{\textrm{rot2}}^2)$}

\State $p_3 \gets$ \Call{prop}{$\delta_{\textrm{rot2}}- \hat\delta_{\textrm{rot2}}, \alpha_1 \hat\delta_{\textrm{rot2}}^2+\alpha_2 \hat\delta_{\textrm{trans}}^2$}

\return $p_1\cdot p_2\cdot p_3$

\EndProcedure
\Procedure{prop-normal-distribution}{$q,\sigma$}
\Return $\frac{1}{\sqrt{2\pi \sigma}}\exp\left(-\frac{1 q}{2\sigma}\right)$
\EndProcedure
\Procedure{prop-triangle-distribution}{$a,b$}
\Return $\max\left\{0, \frac{1}{b\sqrt{6}} - \frac{|a|}{6b}\right\}$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Die beiden Funktionen $\text{prop-normal-distribution}$ und $\text{prop-triangle-distribution}$ bekommen einen einen Punkt $q$ bzw. $a$ und eine Standardabweichung $\sigma$ bzw. $b$. Die Rückgabe ist dann die Wahrscheinlichkeit mit der Punkt $q$ von der Normalverteilung $\mathcal N(0,\sigma)$ bzw. von der Dreiecksverteilung stammt.

Hier sehen wir ein Beispiel für die Verteilung die durch eine Bewegung entsteht. Die Graustufen beschreiben wie Wahrscheinlich ein Punkt ist. Das wird dadurch ausgerechnet das für alle möglichen Punkte die Wahrscheinlichkeit berechnet wird.

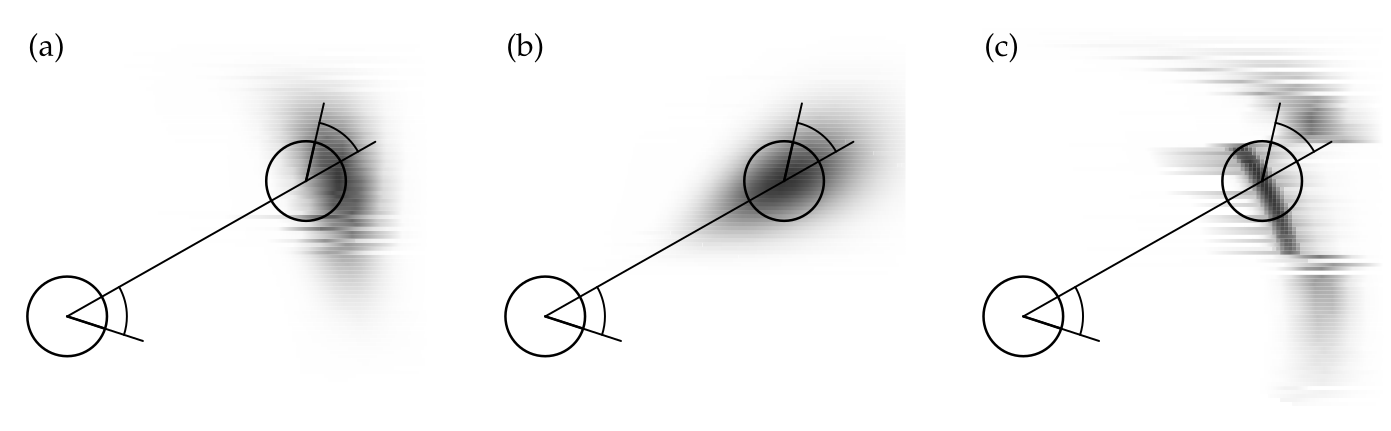
Sampling

Sei $x_{t-1}$ und $u_t$ bekannt. Bei manchen Methoden (z.B. particle filter) reicht es von der Verteilung $p(x_t\mid x_{t-1}, u_t)$ eine Stichprobe zu ziehen. Es werden also nur wahrscheinliche Kandidaten für $x_t$ basierend auf $x_{t-1}$ zurückgegeben.

\begin{algorithm}
\caption{Odometrisches Bewegungsmodell geschlosse Form}
\begin{algorithmic}
\Input initial pose $x_t$, action $u_t$, hypothesized pose $x_{t-1}$
\Procedure{motion-model-odometry}{$x_t,u_t,x_{t-1}$}

\State $\delta_{\textrm{rot1}} \gets \textrm{atan2}(\bar y'-\bar y, \bar x'-\bar x)-\bar \theta$
\State $\delta_{\textrm{trans}} \gets \sqrt{(\bar x-\bar x')^2+(\bar y-\bar y')^2}$
\State $\delta_{\textrm{rot2}} \gets \bar\theta'-\bar\theta-\delta_{\textrm{rot1}}$

\State $\hat\delta_{\textrm{rot1}} \gets \delta_{\textrm{rot1}}$ - \Call{sample}{$\alpha_1\delta_{\textrm{rot1}}^2 + \alpha_2\delta_{\textrm{trans}}^2$}

\State $\hat\delta_{\textrm{trans}} \gets \delta_{\textrm{trans}}$ - \Call{sample}{$\alpha_3\delta_{\textrm{trans}}^2 + \alpha_4(\delta_{\textrm{rot1}}^2 + \delta_{\textrm{rot2}}^2)$}

\State $\hat\delta_{\textrm{rot2}} \gets \delta_{\textrm{rot2}}$ - \Call{sample}{$\alpha_1\delta_{\textrm{rot2}}^2 + \alpha_2\delta_{\textrm{trans}}^2$}

\State $x' \gets x + \hat\delta_{trans} \cos(\theta + \hat\delta_{rot1})$

\State $y' \gets y + \hat\delta_{trans} \sin(\theta + \hat\delta_{rot1})$

\State $\delta' \gets \delta + \hat\delta_{rot1} + \hat\delta_{rot2}$

\return $x_{t}=\left( \begin{array}{ccc} x'& y' & \theta' \end{array} \right)^T$

\EndProcedure
\Procedure{sample-normal-distribution}{$\sigma$}
\Return $\frac{1}{2}\sum_{i=1}^{12}\textrm{rand}(-\sigma,\sigma)$
\EndProcedure
\Procedure{sample-triangle-distribution}{$b$}
\Return $\frac{\sqrt{6}}{2}(\textrm{rand}(-\sqrt{b},\sqrt{b})+ \textrm{rand}(-\sqrt{b},\sqrt{b}))$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Hier geben die beiden Funktionen sample* eine Zufallszahl die der der Normalverteilung $\mathcal N(0,\sigma)$ bzw. Dreiecksverteilung folgt.

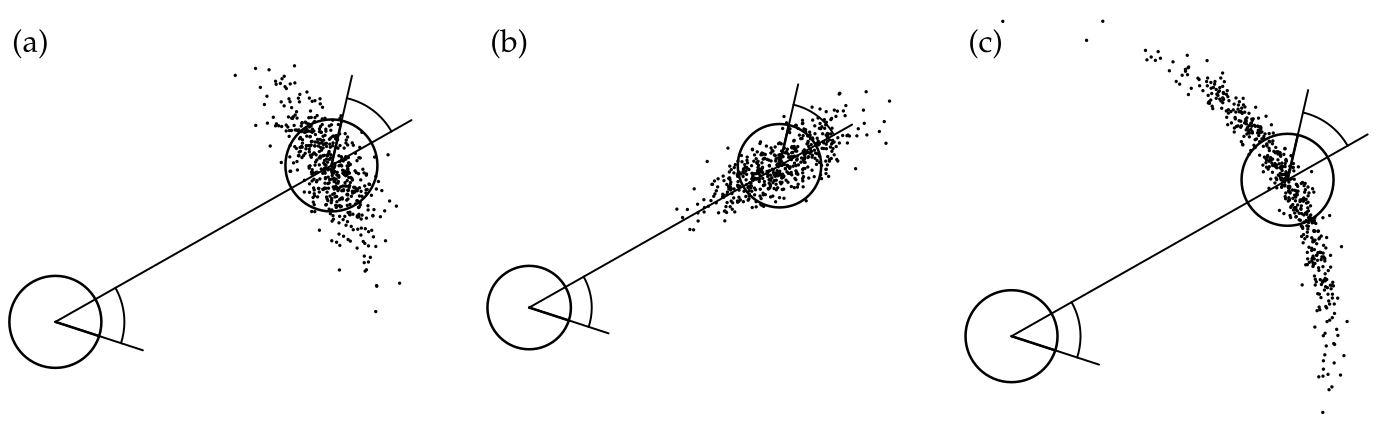Hier sieht man 500 samples zu jeweils einer alpha konfiguration.