Triangulation

Einfache Sprache

Nur Entfernung

Beispiel 2D Raum

Gegeben sein zwei Landmarks $p_1$ und $p_2$, die $a$ voneinander entfernt sind. Nun empfangen wir ein Signal von $p_1$ mit eine Entfernung von $d_1$ und ein Signal von $p_2$ mit einer Entfernung von $d_2$. Was ist unsere Position, hier $x$? Sei $\mathfrak p_1=\left( \begin{array}{cc} 0&0\end{array} \right)^T$ und $\mathfrak p_2=\left( \begin{array}{cc} a&0\end{array} \right)^T$, da kann durch einen Koordinatentransformation (Translation und Rotation) erreicht werden. Dann ist

$$\mathfrak x = \left( \begin{array}{c} \frac{a^2+d_1^2-d_2^2}{2a}\\\pm\sqrt{d_1^2-\left(\frac{a^2+d_1^2-d_2^2}{2a}\right)^2}\end{array} \right)$$

Nur Peilung

Ohne Unsicherheit

Man erhält die Entfernungen der Punkte die man dann nach dem oberen Verfahren in die eigene Position umwandeln kann.

Beispiel im 2D-Raum

Sei nur der Winkel $\Phi$ zwischen 2 Landmarks $A,B$ gegeben so kann die eigene Position $N$ nicht verortet werden! Ist der Winkel $\Psi$ zu einem zusätzlichen Landmark $C$ bekannt, so kann $N$ wie folgt lokalisiert werden. Für eine konkrete Lösung wenden wird Kosinussatz. Für jedes Landmark-Paarkombination setzen wir eine Gleichung nach dem Kosinussatz auf. Die Beschriftung folgt dieser Skizze Es ergibt sich folgendes Gleichungssystem:

$$\begin{align}D_1^2 &= z_1^2+z_2^2-2z_1z_2\cos\alpha\\D_2^2 &= z_2^2+z_3^2-2z_2z_3\cos\beta\\D_3^2 &= z_1^2+z_3^2-2z_1z_3\cos(\alpha+\beta)\\\end{align}$$

Es hat 3 Unbekannten für 3 Gleichungen und kann daher gelöst werden.

Mit Unsicherheit

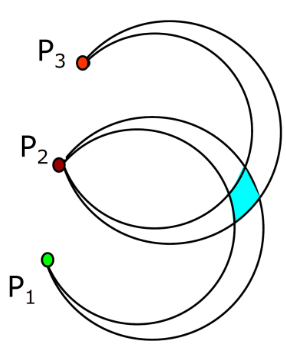
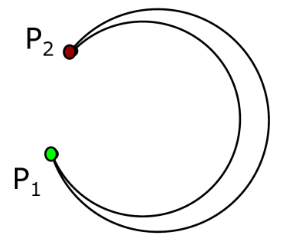
Gib es nicht einen Wert sondern eine Interval für den Winkel so erhält man als mögliche Fläche eine Halbmond.
Für 2 Landmarks ergibt sich folgendes Bild Für 3 Landmarks ergibt sich folgendes Bild. Hier können wir die Position auf die blaue Fläche begrenzen.