Home | Wissen Stichwortverzeichnis Tags

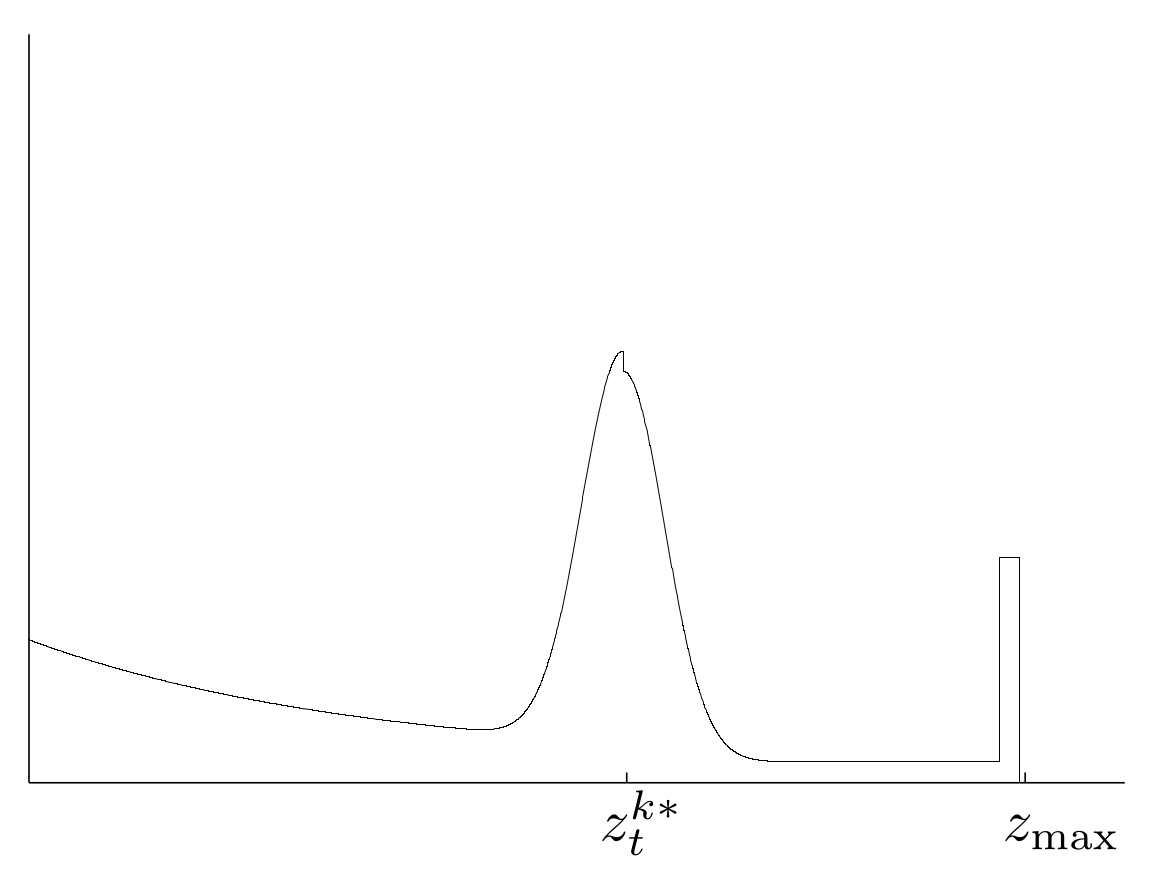
Beam-based sensor model

Einfache Sprache

Die Beam-based sensor model ist ein Wahrscheinlichkeitstheoretische Wahrnehmungsmodelle für Range Finders.

Herleitung

Das Modell berücksichtigt das Modell 4 Fehlerarten:

  1. Messfehler um das erwartete Objekt herum,
  2. Messung unerwartete Objekte,
  3. Verfehlen des erwarteten Objekts und
  4. zufälliger Messfehler. Die Wahrnehmungswahrscheinlichkeit $p(z_t\mid x_t,m)$ ist somit eine Kombination der 4 Verteilungen (Verteilung) die den jeweiligen Fehler beschreiben.

Begriffe

Sei $z_t^{k*}$ die tatsächliche Entfernung des nähsten Objekts und $z_t^{k}$ die gemessen Entfernung. $z_t^{k*}$ kann in Lagegestützte Karte durch ray casting und in Merkmalgestützte Karte Suche des nähstes Objekts in einem Kegel (Winkel) gefunden werden. Sei $z_\textrm{max}$ die maximale Entfernung die der Senor messen kann.

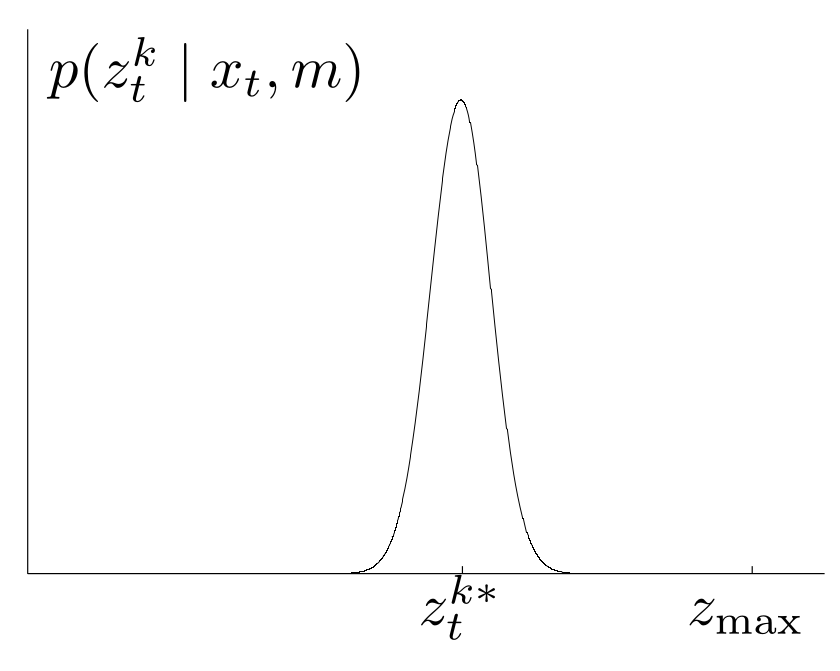
1. Korrekte Messung mit Messungenauigkeit

Da Messungen um die tatsächliche Entfernung kleine Abweichungen aufweist aus verschiedenen Gründen, so z.B. geringe Auflösung des Sensors, wir eine Normalverteilung an mit Erwartungswert $z_t^{k*}$ und Standardabweichung $\sigma_\textrm{hit}$. Wird $z_\mathrm{max}$ beachtet so ergibt sich folgende Verteilung

$$p_\mathrm{hit}(z_t^k\mid x_t,m)=\begin{cases}\eta\,\mathcal N(z_t^k;z_t^{k*}, \sigma_\mathrm{hit}^2)& \mathrm{if}\; 0 \leq z_t^k\leq z_\mathrm{max}\\ 0 & \mathrm{else} \end{cases}$$

Hier wird $z_t^{k*}$, wie oben beschrieben, aus $x_t$ und $m$ durch ray casting berechnet. $\mathcal N(z_t^k;z_t^{k*}, \sigma_\mathrm{hit}^2)$ ist die Normalverteilung mit Erwartungswert $z_t^{k*}$ und Standardabweichung $\sigma_\mathrm{hit}$, ausgewertet an der Stelle $z_t^k$. Also

$$\mathcal N(z_t^k;z_t^{k*}, \sigma_\mathrm{hit}^2) = \frac{1}{\sqrt{2\pi\sigma_\textrm{hit}^2}}\exp\left(-\frac{1}{2}\frac{(z_t^k-z_t^{k*})^2}{\sigma_\textrm{hit}^2}\right)$$

mit der Normalisierungskonstante

$$\eta = \left(\int_0^{z_\mathrm{max}}\mathcal N(z_t^k;z_t^{k*}, \sigma_\mathrm{hit}^2)\;dz_t^k\right)^{-1}\;.$$

Hier ist eine Beispielverteilung Beam-based sensor model1.png

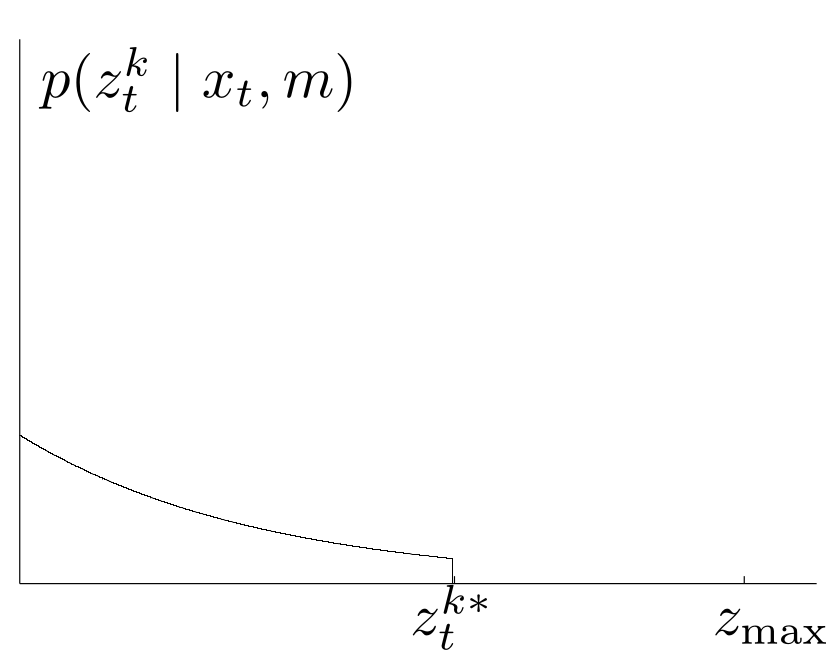
2. Messung unerwarteter Objekte

Hier werden andere bewegliche Objekte, die nicht teil von $m$ sind, berücksichtigt. Diese unmodellierten Objekte haben folgende Eigenschaften:

Die kumulierte Wahrscheinlichkeiten im Interval $[0,z_t^{k*}]$ ist

$$\begin{align}\int_0^{z_t^{k*}}\lambda_\mathrm{short}\exp\left(-\lambda_\mathrm{short} z_t^k\right)\; dz_t^k &= -\exp\left(-\lambda_\mathrm{short}z_t^{k*}\right)+ \exp\left(-\lambda_\mathrm{short}0\right)&\Huge|\normalsize\text{Def. Exponentialverteilung}\\&= 1 -\exp\left(-\lambda_\mathrm{short}z_t^{k*}\right)\\\end{align}$$

womit sich die Normalisierungskonstante als

$$\eta=\frac{1}{1 -\exp\left(-\lambda_\mathrm{short}z_t^{k*}\right)}$$

ergibt. Beam-based sensor model2.png

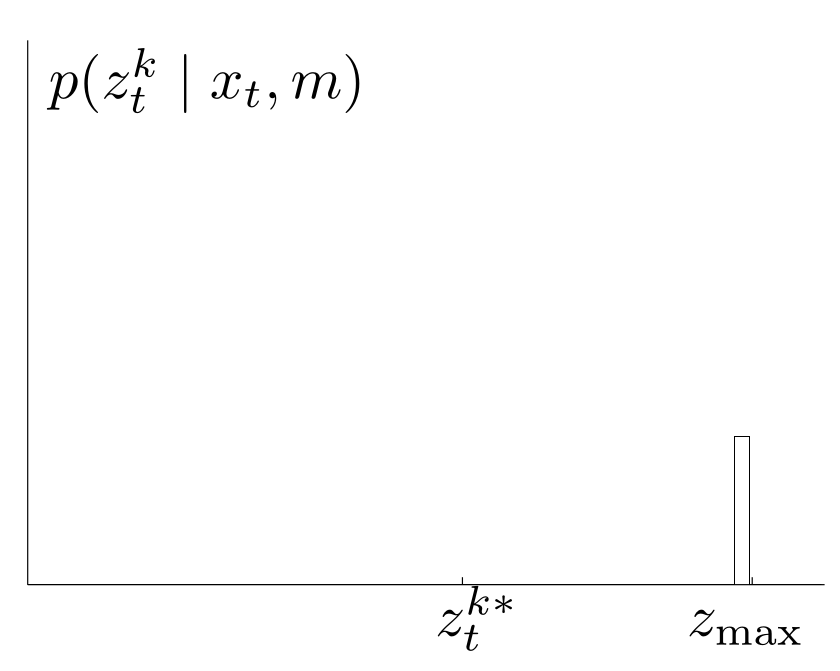
3. Verfehlen

Wird das erwartete Objekt verfehlt, z.B. durch eine Reflexion, ist das Resultat der Wert $z_\textrm{max}$. Zur Modellierung wird eine Indikatorfunktion genutzt die bei $z_\textrm{max}$ ausschlägt. Also

$$p_\mathrm{max}(z_t^k\mid x_t,m)= I(z = z_\textrm{max})= \begin{cases}1& \textrm{if}\; z=z_\textrm{max}\\0&\textrm{else}\end{cases}$$

Beam-based sensor model3.png

4. Zufällige Messfehler

Diese Kategorie umfällst alle restlichen unerklärlichen Messfehler. Wir modellieren es einfach als Uniformverteilung im Interval $[0,z_\textrm{max}]$

$$p_\mathrm{rand}(z_t^k\mid x_t,m)= \begin{cases}\frac{1}{z_\textrm{max}}& \textrm{if}\; 0\leq z_t^k \leq z_\textrm{max}\\0&\textrm{else}\end{cases}$$

Beam-based sensor model4.png

Gesamtverteilung

Die vier oberen Verteilung $p_\textrm{hit}, p_\textrm{short}, p_\textrm{max}$ und $p_\textrm{rand}$ werden nun in einem gewichteten Durchschnitt kombiniert. Dafür verwenden wir die Gewichte $z_\textrm{hit}, z_\textrm{short}, z_\textrm{max}$ und $z_\textrm{rand}$ mit $z_\textrm{hit}+z_\textrm{short}+z_\textrm{max}+z_\textrm{rand} = 1$.

$$p(z_t^k\mid x_t,m)= \left(\begin{array}{c} z_\textrm{hit}\\ z_\textrm{short}\\ z_\textrm{max}\\z_\textrm{rand}\end{array} \right)^T\cdot\left(\begin{array}{c} p_\mathrm{hit}(z_t^k\mid x_t,m)\\ p_\mathrm{short}(z_t^k\mid x_t,m)\\ p_\mathrm{max}(z_t^k\mid x_t,m)\\ p_\mathrm{rand}(z_t^k\mid x_t,m)\end{array} \right)$$

Beispiel Gesamtverteilung

Beam-based sensor model5.png

Algorithmus

1def beam_range_finder_model(z_t, x_t, m, z_hit, z_short, z_max, z_rand, p_hit, p_short, p_max, p_rand, ray_cast):
2    q = 1
3    for k in range(len(z_t)):
4        z_t_k_star = ray_cast(x_t, m, k)
5        p = z_hit * p_hit(z_t[k], x_t, m) + z_short * p_short(z_t[k], x_t, m) + z_max * p_max(z_t[k], x_t, m) + z_rand * p_rand(z_t[k], x_t, m)
6        q *= p
7    return q

\begin{algorithm}
\caption{Entfernungsmessungmodel}
\begin{algorithmic}
\Input measurement $z_t$, pose $x_t$, map $m$
\Procedure{beam-range-finder-model}{$z_t,x_t,m$}
	\State $q \gets 1$
	\For{$k=1$ to $K$}
		\State compute $z_t^{k*}$ for measurement $z_t^k$ using for example ray casting.
		\State $p \gets z_\mathrm{hit}\cdot p_\mathrm{hit}(z_t^k\mid x_t,m) + z_\mathrm{short}\cdot p_\mathrm{short}(z_t^k\mid x_t,m) + z_\mathrm{max}\cdot p_\mathrm{max}(z_t^k\mid x_t,m) + z_\mathrm{rand}\cdot p_\mathrm{rand}(z_t^k\mid x_t,m)$
		\State $q \gets q\cdot p$
    \EndFor
	\return $q$
\EndProcedure
\end{algorithmic}
\end{algorithm}

Parametrisierung

Sei $\Theta$ die Menge der roboterspezifischen Parameter, also die Geweichte $z_\textrm{hit}, z_\textrm{short}, z_\textrm{max}$, $z_\textrm{rand}$ und die Parameter der Verteilungen $\sigma_\mathrm{hit}$ und $\lambda_\mathrm{short}$. Kann durch einen Maximum-Likelihood-Methode aus Daten geschätzt werden.

Tipps

Probleme

Home: