Gleichzeitige Kartierung und Lokalisation
Einfache Sprache
Es sei ein Roboter in einer unbekannten statischen Umgebung gegeben. Der Roboter kann mit Sensoren und Aktoren, sich bewegen und die Umgebung wahrnehmen. Ziel ist es gleichzeitig eine Karte zu erstellen und sich in dieser Karte zu lokalisieren.
Def. Merkmalgestützte SLAM
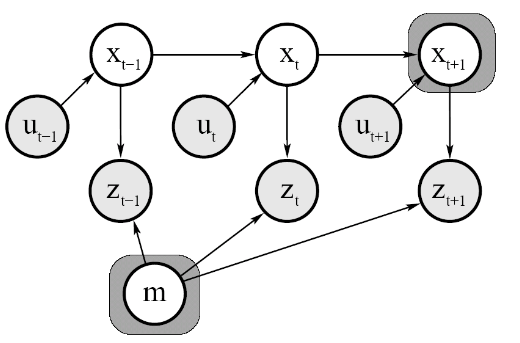
Bei der merkmalgestützten SLAM, im Kontext der Wahrscheinlichkeitstheoretische Robotik, sind die Aktionen $U_{1:k}=\{u_1,\ldots, u_k\}$ und die relativen Wahrnehmungen $Z_{1:k} = \{z_1,\ldots, z_k\}$, wobei sich relativ auf die Position nach den Aktionen bezieht. Ziel ist es eine Karte, genauer einer Merkmalgestützte Karte $m = \{m_1,\ldots,m_n\}$ und den Weg des Roboters $X_{1:k} = \{x_1,\ldots,x_k\}$, wobei $z_i$ in pose $x_i$ aufgezeichnet wurde.
Full SLAM
Der gesamte Roboterpose und Karte wird berechnet. Also
$$p(X_{1:k},m|Z_{1:k},U_{1:k})$$. 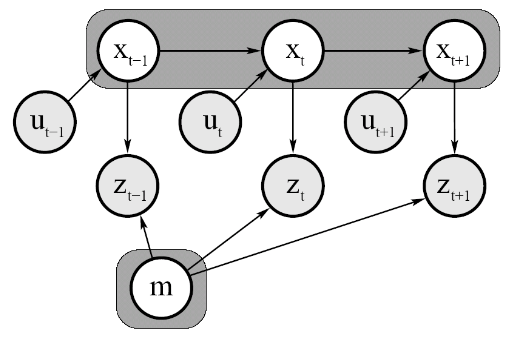
Online SLAM
Der gesamte Roboterpose und Karte wird berechnet. Also
$$p(x_k,m|Z_{1:k},U_{1:k}) = \int\int\ldots\int p(x_k,m|Z_{1:k},U_{1:k})\;dx_1\;dx_2\ldots\;dx_{k-1}$$.