Home | Wissen Stichwortverzeichnis Tags

Markovlokalisation

Einfache Sprache

Def. Markovlokalisation

Abgeleitet vom Bayes-Filter, gegeben ein aktueller Belief $Bel(x_{t-1})$, eine neue Messung $z_t$ und eine durchgeführte Aktion $u_t$ und eine Karte $m$ ist die Markovlokalisation wie folgt definiert

\begin{algorithm}
\caption{Markovlokalisiation}
\begin{algorithmic}
\Input Aktueller Believe Bel$(x_{t-1})$, neue Messung $z_t$, Aktion $u_t$ und Karte $m$
\Procedure{bayesscher-filter}{Bel$(x), z_t, u_t, m$}
	\ForAll{$x_t$}
		\State Bel'$(x_t) = \int p(x_t|u_t,x_{t-1}, m)\text{Bel}(x_{t-1})dx_{t-1}$
		\State Bel$(x_t) = \eta\;p(z_t|x_t,m)\text{Bel'}(x_t)$
	\EndFor
	\Return Bel$(x_t)$
\EndProcedure
\end{algorithmic}
	\end{algorithm}

Startposition

Bei position tracking , mit der der bekannten genauen Startposition $\bar x_0$, wird $\text{Bel}(x_0)$ als Punktmasse-Verteilung wie folgt initialisiert

$$\text{Bel}(x_0)=\begin{cases}1,& x_0=\bar x_0\\0,&x_0\not=\bar x_0\end{cases}\;.$$

Kann die Startposition nur approximiert werden, so wird der Start Belief mit einer Normalverteilung initialisiert

$$\begin{align}\text{Bel}(x_0) &=\mathcal N(x_0;\bar x_0,\Sigma)\\&=\text{det}(2\pi\Sigma)\text{exp}\left(-\frac{1}{2}(x_0-\bar x_0)^T\Sigma^{-1}(x_0-\bar x_0\right)\end{align}\;.$$

Wobei $exp()$ die natürliche Exponentialfunktion ist und $\Sigma$ die Unsicherheit der Startposition.

Bei global tracking ist die Startposition nicht bekannt. Daher wird $\text{Bel}(x_0)$ als Uniformverteilung initialisiert, also

$$\text{Bel}(x_0)=\frac{1}{|X|}\;,$$

wobei $|X|$ das Volumen aller Möglichen Posen ist. Siehe Lebesgue-Maß

Ist nur partielles Wissen über die Startposition gegeben, so kann dies auch benutzt werden. Sei z.B. bekannt das der Roboter in der nähe einer Tür startet. Dann kann einer Verteilung benutzt werden die $0$ ist außer an Stellen die sich in der Nähe einer Tür befinden.

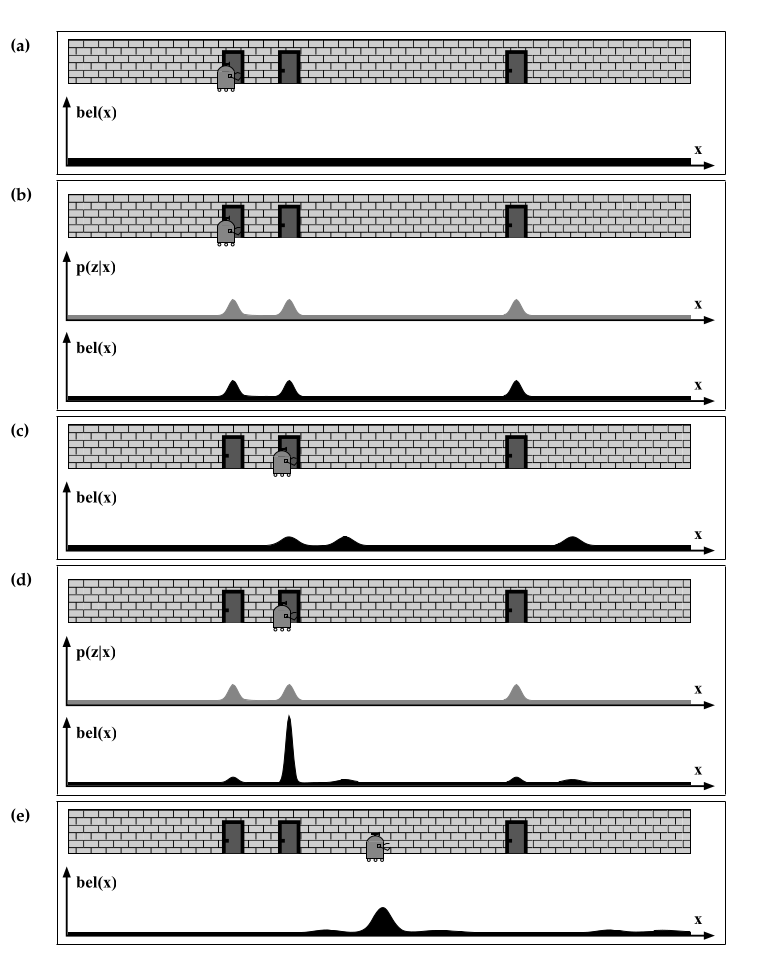
Beispiel

Gezeigt wird eine Markovlokalisation. Erklärung:

Home: