Roboterplannung
Einfache Sprache
Die Hauptziele sind:
- Kollisionsfreie Bewegung und
- Schnelles Erreichen des Ziels.
Dafür muss zum einen der Optimale Weg berechnet werden und auf unvorhergesehene Ereignisse reagiert werden. Meist wird das Problem mit der Klassischen Zwei-Ebenen Architektur für Roboterplannung gelöst.
[Planning is] eminently necessary since, by definition, a robot accomplishes tasks by moving in the real world.
- Latombe (1991)
Def. Roboterbewegungsplannungsproblem
Sei eine Start-Roboterpose $q_I$, eine Ziel-Roboterpose $y_G$, eine geometrische Beschreibung des Roboters und der Umgebung gegeben. Finde den Weg, der den Roboter von $q_I$ nach $q_G$ bringt, ohne ein Hindernis zu berühren.
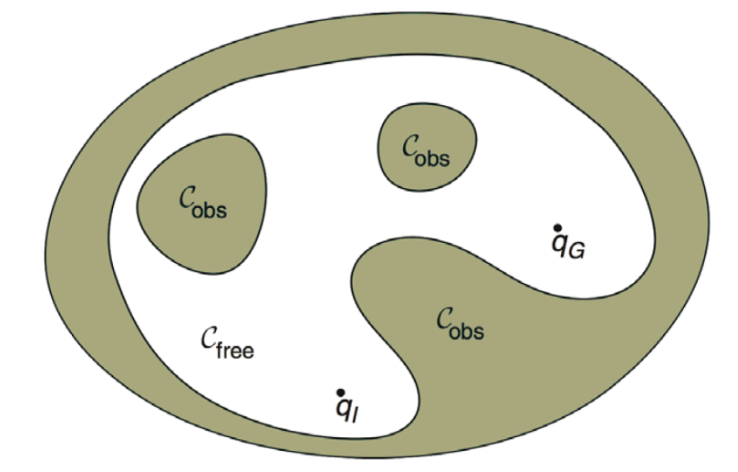
Das Problem wir meist im Konfigurations Raum $\mathcal W$ gelöst. Das ist der Raum, der alle Möglichen Roboterposen umfässt. Also nicht nur den Roboterort sondern auch die Roboterkonfiguration. $\mathcal O \in\mathcal W$ ist die Menge der Hindernisse. $\mathcal A(q)$ ist der Roboter in der Pose $q\in\mathcal C$. Dann ist der freie Konfigurationsraum $\mathcal C_\mathrm{free}$ und der durch Hindernisse besetzte Konfigurationsraum $\mathcal C_\mathrm{obs}$ wie folgt definiert
$$\mathcal C_\mathrm{free} = \{q\in\mathcal C\mid \mathcal A(q)\cap\mathcal O=\emptyset\}$$und
$$\mathcal C_\mathrm{obs}=\mathcal C\setminus\mathcal C_\mathrm{free}\;.$$Das kann z.B. folgendes Bild entstehen
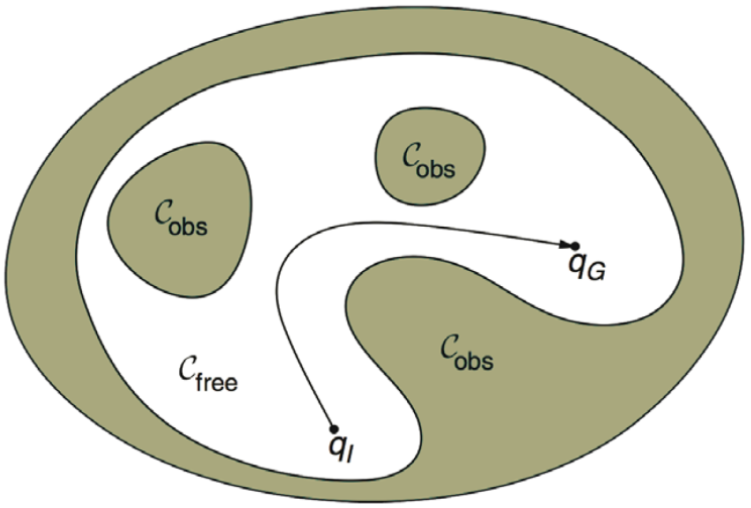
Ziel ist es nun einen kontinuierlichen Weg $\tau$, in Form einer Funktion $\tau:[0,1]\to\mathcal C_\mathrm{free}$ , zu finden, wobei $\tau(0)=q_I$ und $\tau(1)=q_G$.
Das kann, ausgehend vom Bild oben, z.B. so ausehen
Lösung
Das Problem kann entweder Informed Search oder Uninformed Search sein.