Autoregressives Modell
Einfache Sprache
Bei einem autoregressiven Modell setzt sich der Output linear aus früheren Werten und einer Zufallsvariable zusammen.
AR(1) ohne Konstante
Aufbau
Das Autoregressives Modell erster Ordnung ohne Konstante ist das einfachste AR-Modell und wie folgt definiert
$$y_t = a y_{t-1}+\varepsilon_t\;.$$Wobei der Rauschterm $\varepsilon_t$ ein Weißes Rauschen mit Erwartungswert $\text E[\varepsilon_t] = 0$, Varianz $\text{Var}(\epsilon_t) = \sigma^2$ und der Autokovarianz $\text{Cov}(\varepsilon_t,\varepsilon_s) = 0\quad \forall s\not=t\;.$ Durch rekursives Einsetzen der Definition erhält man
$$\begin{align}y_t &= a y_{t-1}+\varepsilon_t &\Huge|\normalsize\text{Def. $y_t$}\\&= a(a y_{t-2}+\varepsilon_{t-1})+\varepsilon_t &\Huge|\normalsize\text{Def. $y_{t-1}$}\\&= a^2 y_{t-2}+a\varepsilon_{t-1}+\varepsilon_t &\Huge|\normalsize\text{Ausklammern}\\&= a^2(a y_{t-3}+\varepsilon_t)+a\varepsilon_{t-1}+\varepsilon_t &\Huge|\normalsize\text{Def. $y_{t-2}$}\\&= a^3y_{t-3}+a^2\varepsilon_t+a\varepsilon_{t-1}+\varepsilon_t &\Huge|\normalsize\text{Ausklammern}\\&\vdots\\&= \varepsilon_t + a\varepsilon_{t-1}+ a^2\varepsilon_{t-2}+\ldots&\Huge|\normalsize\text{Rekursiv}\\&=\sum^\infty_{i=0}a^i\varepsilon_{t-i}&\Huge|\normalsize\text{Geschlossene Form}\end{align}$$Letzeres ist die MA-Modell representation, weil sie zeigt das $y_t$ ein gewichteter Gleitender Mittelwert aller $\varepsilon$ ist.
Eigenschaften
Zusammenfassung
Ist $|a|<1$ gilt
$$\begin{align}\text E(y_t ) &= 0\\ \text{Var}(y_t) &= \sigma^2\frac{1}{1-a^2} &= \gamma_0\\ \text{Var}(y_t,y_{t-k}) &= \sigma^2\frac{a^k}{1-a^2} &= \gamma_k\\\text{Corr}(y_t,y_{t-k}) &= \frac{\gamma_k}{\gamma_0} &= a^k \end{align}$$Dabei impliziert $|a|<1$, dass der Erwartungswert und die Varianz konstant und endlich sind. Es handelt sich als um eine Schwach stationäre Folge. Der Effekt von $\varepsilon_{t-k}$ auf $y_t$ wird mit größer werdender Distanz $k$ immer kleiner. Bis sie Null sind. Daher nimmt auch die Autokorrelation mit steigender Distanz $k$ ab.
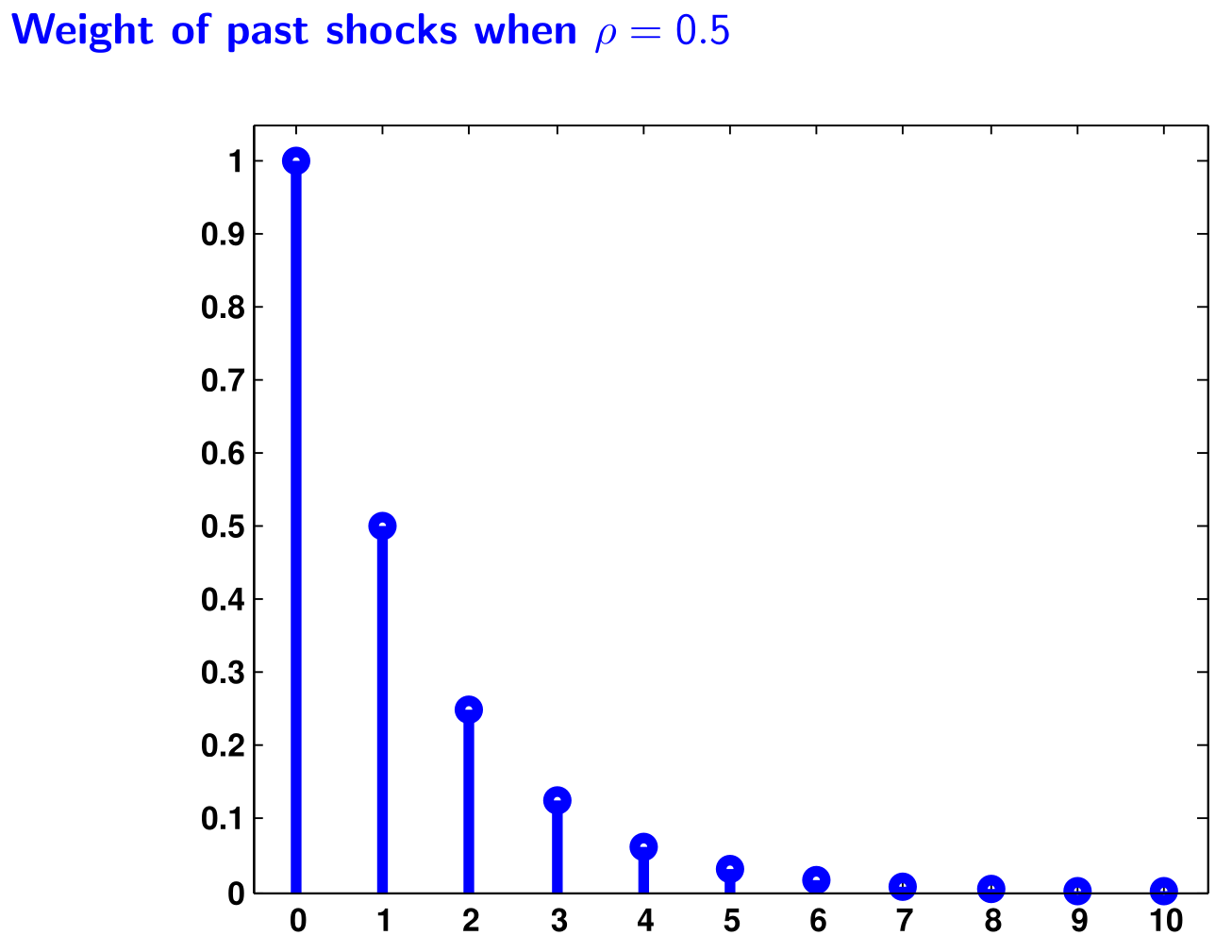
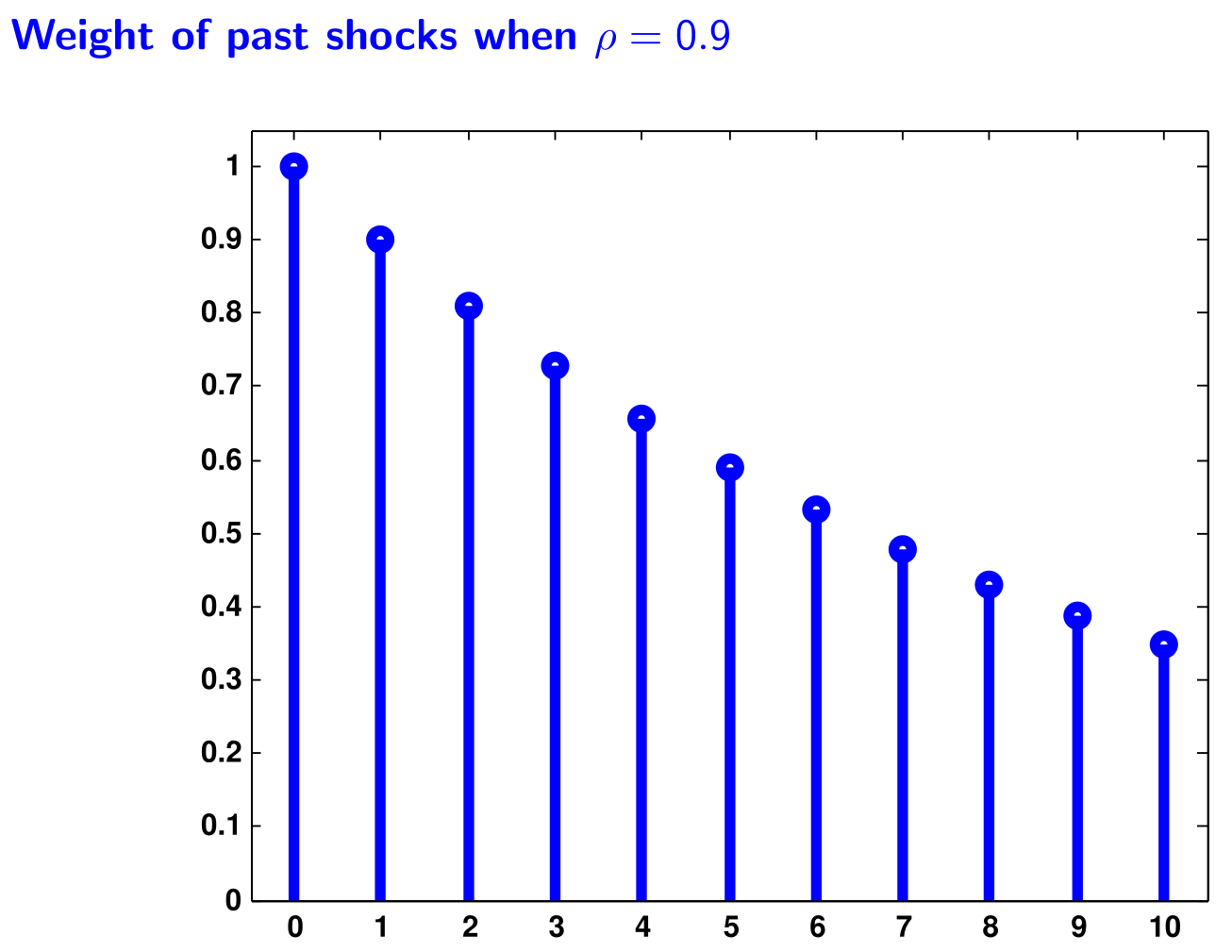
Herleitung
Erwartungswert
Der bedingte Erwartungswert des AR(1) ist gegeben durch
$$\text E[y_{t+1} |y_{t}] = ay_{t} + \text E[\varepsilon_{t+1} |y_{t}] = ay_{t}\;.$$Der Erwartungswert für $s$-Perioden in der Zukunft
$$\text E[y_{t+s} |y_{t}] = a\text E[y_{t+s-1} |y_{t}] + \text E[\varepsilon_{t+s} |y_{t}] = a^sy_{t}\;.$$erhält man durch rekursives Einsetzen.
Der unbedingte Erwartungswert des AR(1) ist gegeben durch
$$\begin{align}\text E[y_t] &= \text E \left[\sum^\infty_{i=0}a^i\varepsilon_{t-i} \right]&\Huge|\normalsize\text{Def. $y_t$ (MA)}\\&= \sum^\infty_{i=0}a^i\text E \left[\varepsilon_{t-i} \right]&\Huge|\normalsize\text{Eig. E (Summe)}\\&= \sum^\infty_{i=0}a^i0&\Huge|\normalsize\text{Eig. $\varepsilon$}\\&= 0&\Huge|\normalsize\text{Eig. $\sum$}\end{align}$$Varianz
Die bedingte Varianz des AR(1) ist gegeben durch
$$\text{Var}(y_t |y_{t−1}) = \text{Var}(\varepsilon_t |y_{t−1}) = \sigma^2\;.$$Die unbedingte Varianz des AR(1) ist gegeben durch
$$\text{Var}(y_t) = \sigma^2\frac{1}{1-a^2} = \gamma_0\;,$$wobei $\gamma_0$ für doe Autokovarianz der Ordnung $0$ steht. Verallgemeinert ergibt sich für die Autokovarianzen
$$\text{Var}(y_t,y_{t-k}) = \sigma^2\frac{a^k}{1-a^2} = \gamma_k\;.$$Daraus ergibt folgende Autokorrelation
$$\text{Corr}(y_t,y_{t-k}) = \frac{\gamma_k}{\gamma_0} = a^k\;.$$Schätzung
Das AR(1) ohne Konstante ist gegeben durch
$$\hat\alpha =(Y_{-1} Y_{-1})^{-1}Y_{−1}Y = \left(\sum_{t=2}^{T}y^2_{t-1}\right)^{-1}\sum_{t=2}^{T}y_{t-1}y_{t}\;.$$OLS yields again a consistent and asymptotically normally distributed estimator as long as the disturbance et is not autocorrelated. Otherwise, the estimator is inconsistent.
AR(1) mit Konstante
Aufbau
Das Autoregressives Modell erster Ordnung mit Konstante ist wie folgt definiert
$$y_t = \mu + a y_{t-1}+\varepsilon_t\;.$$Eigenschaften
Damit die Folge Schwach stationär ist muss ergibt sich
$$\begin{align}\text E[y_t] &= \text E \left[\mu + a y_{t-1}+\varepsilon_t \right]&\Huge|\normalsize\text{Def. $y_t$}\\&= \text E [\mu] + \text E [a y_{t-1}]+\text E [\varepsilon_t ]&\Huge|\normalsize\text{Eig. E (Summe)}\\&= \mu + a\text E [y_{t-1}]+\text E [\varepsilon_t ]&\Huge|\normalsize\text{Eig. E (Unabhängig)}\\&= \mu + a\text E [y_{t-1}]&\Huge|\normalsize\text{Eig. $\varepsilon_t$}\\&= \mu + a\text E[y_{t}]&\Huge|\normalsize\text{Schwach stationär}\\\text E[y_t] -a\text E[y_t]&= \mu &\Huge|\normalsize\text{Umformen}\\(1-a)\text E[y_t]&= \mu &\Huge|\normalsize\text{Ausklammern}\\\text E[y_t]&= \frac{\mu}{1-a} &\Huge|\normalsize\text{Umformen}\end{align}$$Da der stochastische Teil ungeändert ist im Vergleich zum AR(1) ohne Konstante sind die restlichen Eigenschaften gleich.
Schätzung
Gleich wie mit ohne Konstante.
AR(p)
Aufbau
Das Autoregressives Modell der Ordnung $p$ ist das einfachste AR-Modell und wie folgt definiert
$$y_t = \mu +a_1 y_{t-1}+\ldots+a_p y_{t-p}+\varepsilon_t\;.$$Wobei $\varepsilon_t$ ein Weißes Rauschen mit Erwartungswert $\text E[\varepsilon_t] = 0$, Varianz $\text{Var}(\epsilon_t) = \sigma^2$ und der Autokovarianz $\text{Cov}(\varepsilon_t,\varepsilon_s) = 0\quad \forall s\not=t\;.$ Durch umstellen der Definition erhält man die Schreibweise als Lag-Polynom
$$\begin{align}y_t-a_1 y_{t-1}-\ldots-a_p y_{t-p} &= \mu+\varepsilon_t\\a(L)y_t &= \mu+\varepsilon_t\end{align}$$Achtung: Hier ist $a(L)$ als $1 − a_1 L − \cdots − a_p L^p$ definiert.
Eigenschaften
Zusammenfassung
Unter der Annahme der Stationärität ergibt sich als Erwartungswert
$$ a(1)E(y_t) = \mu\;.$$Herleitung
Erwartungswert
Unter der Annahme der Prozess ist Stationär ergibt sich folgender Erwartungswert
$$\begin{align}E(y_t )- a_1 E(y_{t-1})-\ldots- a_p E(y_{t-p} ) &= \mu + E(e_t )&\\E(y_t)- a_1 E(y_{t})-\ldots- a_p E(y_{t} ) &= \mu &\Huge|\normalsize\text{Eig. $\varepsilon$ \& stationär}\\ a(1)E(y_t) &= \mu &\Huge|\normalsize\text{Def. Lag-Polynom}\\c&\Huge|\normalsize\text{Umstellen}\\\end{align}$$Schätzung
Seien $T$ Beobachtungen gegeben und soll ein AR(p)-Modell mit Methode der kleinsten Quadrate. Die Beobachtungen seien in folgender Form als Vektor und Matrix gegeben:
$$ \mathfrak y = \left( \begin{array}{c} y_{p+1}\\ \vdots\\y_T \end{array} \right)$$und
$$ \mathfrak Z = \left( \begin{array}{cccc}1 & y_p& \ldots & y_1\\ \vdots& \vdots& & \vdots\\ 1 & y_{T-1}& \ldots & y_{T-p}\end{array} \right)\;.$$Die Schätzer erhalten wir durch
$$\left( \begin{array}{c} \hat\mu\\ \hat a_1\\\vdots\\\hat a_p \end{array} \right) = (\mathfrak Z'\mathfrak Z)^{-1}\mathfrak Z'\mathfrak y\;.$$Wenn $\varepsilon$ Weißes Rauschen ist, dann sind die Schätzer Konsistent und asymtotisch normalverteilt.