Golden Rule
Einfache Sprache
Die Golden Rule besagt, dass die Sparquote $s$ so zuwählen ist, dass der Konsum $c$ maximiert wird. Daraus folgt das ein bestimmtes Konsumniveau $c_g$, welches maximal erreicht werden kann.
Def. Golden Rule
Der pro-Kopf Konsum der aus der Golden Rule folgt ist gegeben durch
$$c_g = f(k_g)-(n+\delta)k_g\;.$$Wobei $k^*$ welcher $c^*$ maximiert als $k_g$ bezeichnet wird und definiert wird durch
$$f'(k_g)=n+\delta\;.$$
Herleitung
Wir definieren die optimal pro-Kopf zu konsumierende Menge $c^*$ in Abhängigkeit von der Sparquote $s$. Zunächst gilt
$$c^*(s) = (1-s)f(k^*(s))\;.$$Da wir auf einem BGP seien müssen gilt $sf(k^*) = (n+\delta)k^*$. Daraus folgt
$$c^*(s) = f(k^*(s))-(n+\delta)k^*(s)\;.$$Um jetzt zu Minimieren leiten wir nach $s$ ab und setzten gleich Null
$$\frac{\partial c^*(s)}{\partial s} = \left(f'(k^*(s))-(n-\delta)\right)\frac{\partial k^*(s)}{\partial s} = 0\;.$$Da $\frac{\partial k^*(s)}{\partial s}>0$ ist muss $f'(k^*(s))-(n-\delta) = 0$ gelten. Die optimale Kapitalintensität muss also folgende Bedingung erfüllen
$$f'(k_g)=n+\delta\;.$$Ist $k_g$ einmal bestimmt, kann daraus $c_g$ wie folgt bestimmt werden
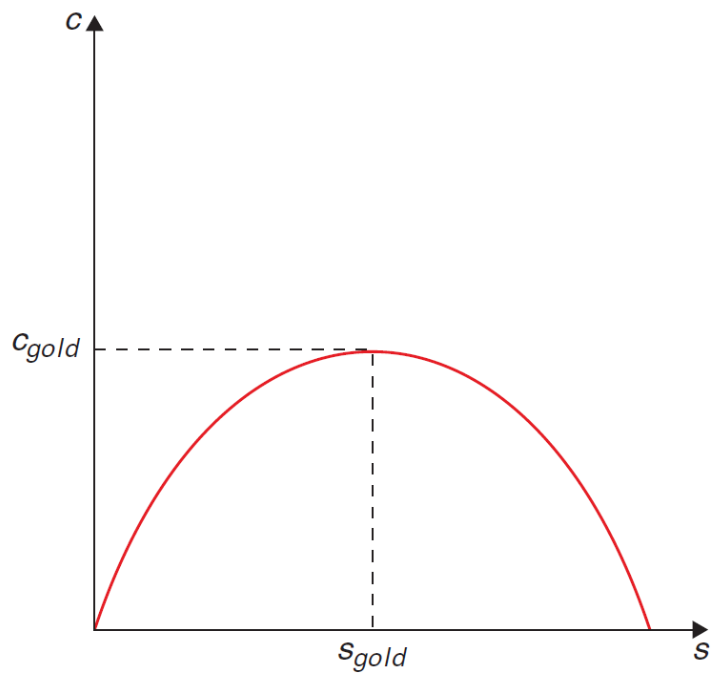
$$c_g = f(k_g)-(n+\delta)k_g\;.$$Grafisches Beispiel
Da $f(k^*(s))$ Konkav und $(n+\delta)k^*(s)$ linear ist ergibt sich folgendes Bild: