Solow-Modell mit Humankapital
Einfache Sprache
Variablen
Variablen
| Symbol | Bedeutung | Formel |
|---|---|---|
| $K$ | Kapital | |
| $L$ | Arbeit | |
| $E_t$ | Humankapital | $L_t\cdot e^{\lambda t}$ |
| $A$ | Technologie | |
| $Y$ | Output | |
| $H$ | Humankapital | |
| $s$ | Sparquote | |
| $\delta$ | Abschreibungsquote | |
| $C$ | Konsum | |
| $I$ | Investition | |
| $T$ | Technologie | |
| $k$ | Kapitalintensität | $K/L$ |
| $y$ | Produktionsertrag pro Arbeitseinheit | $Y/L$ |
| $\gamma_k$ | Wachstumsrate der Kapitalintensität | |
| $k^*$ | Variablen auf einem BGP z.B. Kapitalintensität $k$ | |
| $k_g$ | Optimaler Kapitalintensität pro Kopf nach der Golden Rule | |
| $c_g$ | Optimaler Konsum pro Kopf nach der Golden Rule | |
| $n$ | Bevölkerungswachstum | |
| $s_k$ | Sparquote für Kapital | |
| $s_h$ | Sparquote für Humankapital |
- Variablen mit einem Punkt drüber sind die Differenzen bezüglich der Zeit, z.B. $\dot K = K/t$.
- Kleinbuchstabige Variablen sind sind die Differenzen bezüglich der Einwohner, z.B. $k = K/L$ aber auch $f = F/L$ (also die Pro-Kopf-Produktionsfunktion).
Annahmen
- Hier wird angenommen das die Rendite der Akkumulation größer als im einfachen Solow-Model. Es kann in diesem Modell nicht nur in physische Kapital sondern auch in Humankapital investiert werden.
Aufbau
Wir nehmen folgende Cobb-Douglas-Funktion für das Modell an
$$Y = K^\alpha H^\beta (AL)^\gamma\;.$$Hier wird angenommen, dass die Technologie $A$ sich ausschließlich auf die Produktivität der Arbeit auswirkt.
Form der Produktionsfunktion
In diesem Fall gilt
$$Y = A_1K^\alpha H^\beta L^\gamma\ \iff Y = K^\alpha H^\beta (A_2L)^\gamma$$genau dann wenn $A_1 \equiv A_2^\gamma$. Wir können einfach ausgehen das dies so möglich ist. Um einen BGP zu finden ist es aber wichtig das die Technologie $A$ sich auf die Arbeit auswirkt und deshalb wird diese Produktionsfunktion gewählt.
Durch das Teilen von durch $L$ erhalten wir
$$\begin{align}&\frac{Y}{L} = A^\gamma\frac{K^\alpha H^\beta L^\gamma}{L}\\ \iff&\frac{Y}{L} = A^\gamma\frac{K^\alpha H^\beta L^\gamma L^\alpha L^\beta}{L^\alpha L^\beta L}&\Huge|\normalsize\text{Bruch erweitern.}\\ \iff&\frac{Y}{L} = A^\gamma \left(\frac{K}{L}\right)^\alpha \left(\frac{H}{L}\right)^\beta L^{\alpha + \beta +\gamma -1}&\Huge|\normalsize\text{Umstellen.}\\ \end{align}$$Wobei $\alpha +\beta+\gamma$ bestimmt die Art des Skalenertrags.
- Gilt $\alpha +\beta+\gamma = 1$ dann haben wir Konstante Skalenerträge.
- Gilt $\alpha +\beta+\gamma > 1$ dann haben wir Zunehmende Skalenerträge. Wir nehmen $\alpha +\beta+\gamma = 1$ an und schreiben die Funktion mit pro-Kopf Variablen: $$y = A^\gamma k^\alpha h^\beta\;.$$
Fundamentale Bewegungsgleichung
Wie im einfachen Solow-Modell gehen wir von Fundamentale Bewegungsgleichung des Solow-Modells aus. Hier wird aber in Sparquote für Kapital $s_k$ und $s_h$ unterschieden so, dass
$$\begin{align}\dot K = s_kY-\delta K,\\\dot H = s_hY-\delta H.\end{align}$$Analog zur Herleitung der Fundamentale Bewegungsgleichung erhalten wir
$$\begin{align}\dot k = s_kA^\gamma k^\alpha h^\beta-(\delta+n) k,\\\dot h = s_hA^\gamma k^\alpha h^\beta-(\delta+n) h.\end{align}$$Daraus ergeben sich folgende Wachstumsrate
$$\begin{align}\gamma_k = \frac{\dot k}{k} = s_kA^\gamma k^{\alpha-1} h^\beta-\delta-n,\\\gamma_h = \frac{\dot h}{h} = s_hA^\gamma k^\alpha h^{\beta-1}-\delta-n\;.\end{align}$$Balanced growth path
Im BGP müssen alle Variablen mit konstanter Größe wachsen. Das ist gegeben wenn
$$\begin{align}(\alpha-1)\gamma_k+\beta\gamma_h&=0,\\\alpha\gamma_k+(\beta-1)\gamma_h&=0. \end{align}$$Herleitung
Wir nutzen zunächst die Definition der stetigen Wachstumsrate angewandt auf unser Problem
$$\gamma_{\gamma_k} = \frac{1}{\gamma_k}\cdot\frac{\partial\gamma_k}{\partial t}\;.$$Da $\gamma_k$ von $k$ und $h$ abhängt, ergibt sich die Ableitung (kettenregel) von $\gamma_k$ wie folgt
$$\frac{\partial\gamma_k}{\partial t} = \frac{\partial\gamma_k}{\partial k}\frac{\partial k}{\partial t}+\frac{\partial\gamma_k}{\partial h}\frac{\partial h}{\partial t}\;.$$Einzelnen Ableitungen lassen sich einfach ermitteln als
$$\begin{align}\frac{\partial\gamma_k}{\partial k} &=(\alpha-1)s_kA^\gamma k^{\alpha-2} h^\beta\\\frac{\partial\gamma_k}{\partial h} &= \beta s_kA^\gamma k^{\alpha-1} h^{\beta-1}\\\frac{\partial k}{\partial t} &= \gamma_k k\\\frac{\partial h}{\partial t} &= \gamma_h h\\\end{align}$$Zusetzlich nutzen wir den Fakt das
$$\gamma_k = s_kA^\gamma k^{\alpha-1} h^\beta-\delta-n \iff s_kA^\gamma k^{\alpha-1} h^\beta = \gamma_k + \delta+ n$$bzw.
$$\gamma_h = s_hA^\gamma k^\alpha h^{\beta-1}-\delta-n \iff s_hA^\gamma k^\alpha h^{\beta-1} = \gamma_h + \delta+ n$$Damit ist
$$\begin{align}\gamma_{\gamma_k} &= \frac{1}{\gamma_k}\cdot\frac{\partial\gamma_k}{\partial t} &\Huge|\normalsize\text{Def. $\gamma_{\gamma_k}$}\\&= \frac{\frac{\partial\gamma_k}{\partial k}\frac{\partial k}{\partial t}+\frac{\partial\gamma_k}{\partial h}\frac{\partial h}{\partial t}}{\gamma_k}&\Huge|\normalsize\text{Def. $\frac{\partial\gamma_k}{\partial t}$}\\&= \frac{(\alpha-1)s_kA^\gamma k^{\alpha-2} h^\beta\gamma_k k + \beta s_kA^\gamma k^{\alpha-1} h^{\beta-1}\gamma_h h}{\gamma_k}&\Huge|\normalsize\text{Def. oben}\\&= \frac{(\alpha-1)s_kA^\gamma k^{\alpha-1} h^\beta\gamma_k + \beta s_kA^\gamma k^{\alpha-1} h^{\beta}\gamma_h}{\gamma_k}&\Huge|\normalsize\text{Vereinfachen}\\&= \frac{(\alpha-1)(\gamma_k + \delta+ n)\gamma_k + \beta (\gamma_k + \delta+ n)\gamma_h}{\gamma_k}&\Huge|\normalsize\text{Def. Oben}\\&= \frac{(\gamma_k + \delta+ n)((\alpha-1)\gamma_k + \beta\gamma_h)}{\gamma_k}&\Huge|\normalsize\text{Ausklammern}\\\end{align}$$Wir setzen nun $\gamma_{\gamma_k} = 0$, da am BGP $k$ mit konstanter große wächst. Dabei nutzen wir den Fakt das $\frac{\gamma_k+\delta+n}{\gamma_k}\not=0$. Dadurch bekommen wir die Bedingung
$$(\alpha-1)\gamma_k+\beta\gamma_h=0$$für einen BGP. Analog lässt es sich auf für $\gamma_h$ vorgehen.
Durch einsetzen der zweiten Gleichung, nach $\gamma_h$ umgestellt
$$\gamma_h = \frac{\alpha}{1-\beta}\gamma_k\;,$$in die erste Gleichung erhalten wir
$$\begin{align}(\alpha-1)\gamma_k+\beta\gamma_h&=0&\\ (\alpha-1)\gamma_k+\beta\frac{\alpha}{1-\beta}\gamma_k&=0&\Huge|\normalsize\text{Ersetze $\gamma_h$}\\ \left((\alpha-1)+\beta\frac{\alpha}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Ausklammern}\\ \left(\frac{(\alpha-1)(1-\beta)}{1-\beta}+\beta\frac{\alpha}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Erweitern}\\ \left(\frac{\alpha-\alpha\beta-1+\beta}{1-\beta}+\beta\frac{\alpha}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Ausmultiplizieren}\\ \left(\frac{\alpha-\alpha\beta-1+\beta+\beta\alpha}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Bruchrechenen}\\ \left(\frac{\alpha+\beta-1}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Vereinfachen}\\ -\left(\frac{\alpha+\beta-1}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Multi. mit $-1$}\\ \left(\frac{-(\alpha+\beta-1)}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Minus reinziehen}\\ \left(\frac{1- \alpha-\beta}{1-\beta}\right)\gamma_k&=0&\Huge|\normalsize\text{Minus reinziehen}\end{align}$$Wann gibt es also einen BGP?
- Wenn wir von Abnehmende Skalenerträge ausgehen, nehmen wir $\alpha+\beta<1$ an. Daraus folgt $\gamma_k = \gamma_h = 0$. Auf dem BGP gibt es also wieder kein pro-Kopf Wachstum genau so wie im Einfaches Solow-Modell.
- Ähnlich sieht es aus wenn wir von Zunehmende Skalenerträge ausgehen. Also $\alpha+\beta>1$. Wieder folgt $\gamma_k = \gamma_h = 0$ und ein BGP ohne pro-Kopf Wachstum.
- Aber wenn wir $\alpha + \beta = 1$ annehmen, also Konstante Skalenerträge für Kapital und Humankapital zusammen die reproduzierbaren Faktoren, gibt es einen einen BGP mit pro-Kopf Wachstum, also bei dem $\gamma_k>1$. Nun setzen wir von oben $(\alpha-1)\gamma_k+\beta\gamma_h=0$ und $\alpha\gamma_k+(\beta-1)\gamma_h=0$ gleich und erhalten $$\begin{align}(\alpha-1)\gamma_k+\beta\gamma_h &= \alpha\gamma_k+(\beta-1)\gamma_h &\Huge|\normalsize\text{Def. Oben}\\\beta\gamma_h -(\beta-1)\gamma_h&= \alpha\gamma_k- (\alpha-1)\gamma_k &\Huge|\normalsize\text{Umstellen}\\(\beta-\beta+1)\gamma_h&=(\alpha-\alpha+1)\gamma_k &\Huge|\normalsize\text{Ausklammern}\\\gamma_h&=\gamma_k &\Huge|\normalsize\text{Vereinfachen}\\\end{align}$$Die Wachstumsrate von $k$ und $h$ müssen also gleichgroß sein. Da wir nun $\gamma_k = \gamma_h$ wissen können wir das durch deren Definition ersetzen und erhalten dann $$\begin{align}\gamma_k &= \gamma_h \\ s_kA^\gamma k^{\alpha-1} h^\beta-\delta-n &= s_hA^\gamma k^\alpha h^{\beta-1}-\delta-n &\Huge|\normalsize\text{Def. $\gamma_k,\gamma_h$}\\ s_kk^{\alpha-1} h^\beta &= s_hk^\alpha h^{\beta-1}&\Huge|\normalsize\text{Vereinfachen}\\ s_kk^\alpha k^{-1} h^\beta &= s_hk^\alpha h^\beta h^{-1}&\Huge|\normalsize\text{Potenzregeln}\\\ s_k k^{-1} &= s_hh^{-1}&\Huge|\normalsize\text{Vereinfachen}\\\frac{s_k}{s_h}&= \frac{k}{h}&\Huge|\normalsize\text{Umstellen}\\\end{align}$$ Die Interpretation von $\frac{s_k}{s_h} = \frac{k}{h}$ ist, dass das Verhältnis zwischen den zwei Arten von Kapital proportional zum Verhältnis der jeweiligen Sparquoten ist. Also wird im BGP soviel in Kapital bzw. Humankapital investiert, damit deren Wachstumsraten gleich bleiben.
Um die $\gamma_k$ bzw. $\gamma_h$ im BGP zu ermitteln beginnen wir wieder mit deren Definition:
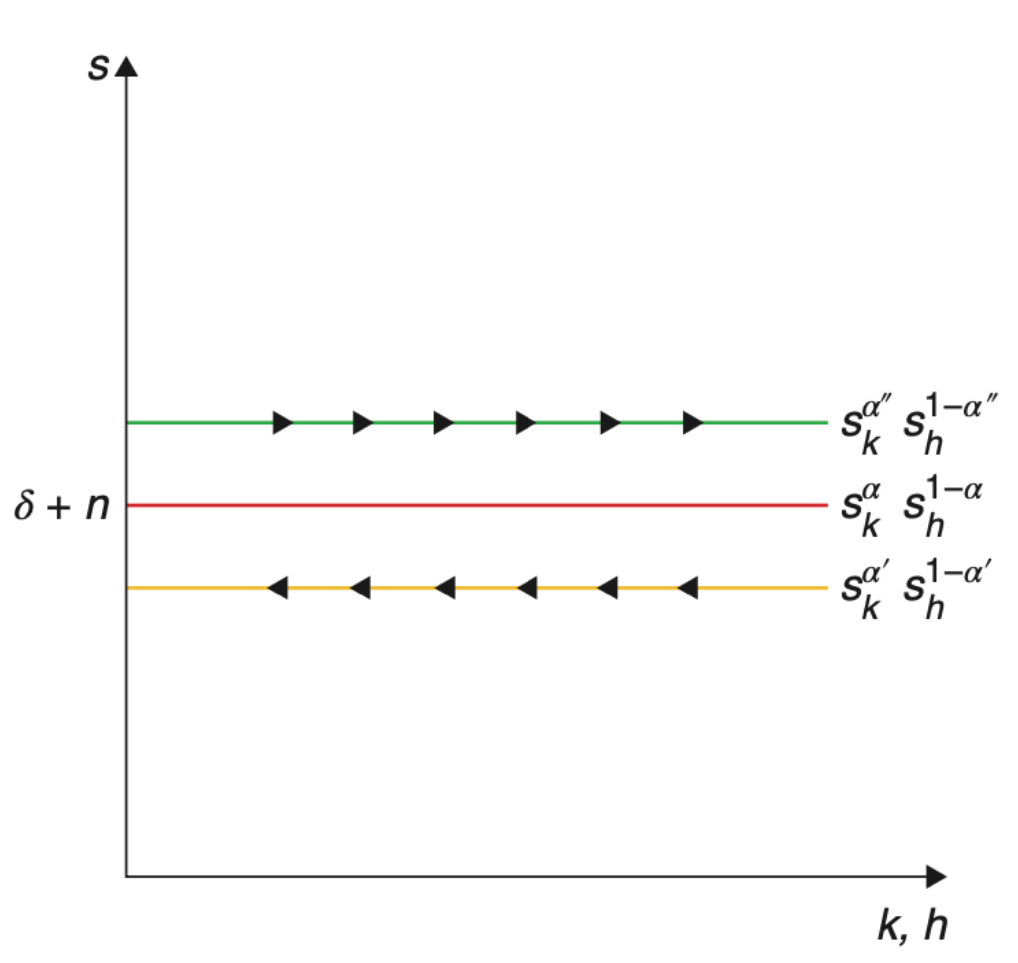
$$\begin{align}\gamma_h &= s_hA^\gamma k^\alpha h^{\beta-1}-\delta-n &\Huge|\normalsize\text{Def. Oben}\\ &= s_hA^\gamma k^\alpha h^{\beta-1}\frac{h^\alpha}{h^\alpha}-\delta-n &\Huge|\normalsize\text{Bruch erweitern}\\ &= s_hA^\gamma \left(\frac{k}{h}\right)^\alpha h^{\beta+ \alpha-1}-\delta-n &\Huge|\normalsize\text{Umstellen}\\ &= s_hA^\gamma \left(\frac{k}{h}\right)^\alpha -\delta-n &\Huge|\normalsize\text{Def. $a+b=1$}\\&= s_hA^\gamma \left(\frac{s_k}{s_h}\right)^\alpha -\delta-n &\Huge|\normalsize\text{Def. Oben}\\&= A^\gamma s_k^\alpha s_h^{1-\alpha} -\delta-n &\Huge|\normalsize\text{Vereinfachen}\\&= \gamma_k &\Huge|\normalsize\text{Def. $\gamma_k = \gamma_h$}\\\end{align}$$Wachstum des Outputs
Wir beginnen mit dem pro-Kopf Output definiert durch $y = A^\gamma k^\alpha h^\beta$. Da wir $\alpha+\beta=1\iff \beta=1-\alpha$ annehmen ergibt sich
$$y = A^\gamma k^\alpha h^{1-\alpha}$$Um die Wachstumsrate des Outputs $\gamma_y$ zu erhalten gehen wir wie folgt vor
$$\begin{align}\gamma_y &= \frac{\frac{\partial y}{\partial t}}{y}&\Huge|\normalsize\text{Def. Wachstumsrate}\\&= \frac{\frac{\partial y}{\partial k}\frac{\partial k}{\partial t}+\frac{\partial y}{\partial h}\frac{\partial h}{\partial t}}{y}&\Huge|\normalsize\text{Produktregel}\\&= \frac{\frac{\partial y}{\partial k}\gamma_kk+\frac{\partial y}{\partial h}\gamma_h h}{y}&\Huge|\normalsize\text{Änderungrate}\\&= \frac{\alpha A^\gamma k^{\alpha-1} h^{1-\alpha}\gamma_kk+(1-\alpha) A^\gamma k^\alpha h^{-\alpha}\gamma_h h}{y}&\Huge|\normalsize\text{Ableitung}\\&= \frac{\alpha A^\gamma k^\alpha h^{1-\alpha}\gamma_k+(1-\alpha) A^\gamma k^\alpha h^{1-\alpha}\gamma_h}{y}&\Huge|\normalsize\text{Potenzregeln}\\&= \frac{(\alpha \gamma_k+(1-\alpha)\gamma_h) A^\gamma k^\alpha h^{1-\alpha}}{y}&\Huge|\normalsize\text{Ausklammern}\\&= \frac{(\alpha \gamma_k+(1-\alpha)\gamma_h) y}{y}&\Huge|\normalsize\text{Def. $y$}\\&=\alpha \gamma_k+(1-\alpha)\gamma_h&\Huge|\normalsize\text{Vereinfachen}\\&=\alpha \gamma_k+(1-\alpha)\gamma_k&\Huge|\normalsize\text{$\gamma_k = \gamma_h$}\\&=(\alpha+(1-\alpha))\gamma_k&\Huge|\normalsize\text{Ausklammern}\\&=\gamma_k&\Huge|\normalsize\text{Vereinfachen}\\&=A^\gamma s_k^\alpha s_h^{1-\alpha} -\delta-n &\Huge|\normalsize\text{Def. $\gamma_k$}\\\end{align}$$Da alle Parameter in $\gamma_y$ Exogen sind haben wir wieder kein Endogenes Wachstum außer wir haben technologische Entwicklung in From von $\gamma_A = g$. Also das $A$ wächst. Dies ist aber dann wieder Endogen gesetzt.
Anwendung
Konvergenz
Da die Wachstumsrate konstant sind, würden die Distanz zwischen Volkswirtschaften mit unterschiedlichen Start-Wachstumsraten über die Zeit immer größer werden. Es gibt Divergenz.