Standard-neoklassisches Wachstumsmodell
Einfache Sprache
Zentralisierte Lösung
Es existiert ein zentraler Planer, welcher das Problem löst.
Variablen
| Symbol | Bedeutung | Formel |
|---|---|---|
| $U$ | Nutzen des repräsentativen Haushalts | |
| $n$ | Bevölkerungswachstum | |
| $\rho$ | Rate der Zeitpräferenz (Ungeduld) | |
| $c$ | pro-Kopf Konsum | |
| $y$ | pro-Kopf Einkommen/Output | |
| $k$ | Kapitalintensität | |
| $f(\cdot)$ | neoklassische Produktionsfunktion | |
| $A$ | technologische Entwicklung (Produktivitätszuwachs) |
Annahmen
- Geschlossene Ökonomie
- Kein Staat
- Nur ein Gut
- Haushalte leben für immer.
- Es existiert ein allwissender Planner.
- $c(t)$ erfüllt Inada-Bedingungen
- $\rho >n$
Aufbau
Problemstellung
Wir nehmen an, dass die Nutzenfunktion des repräsentativen Haushalts wie folgt aussieht
$$U = \int^\infty_0 e^{-\rho t}u(c(t))e^{nt}\,dt\;.$$Da $c(t)$ die Inada-Bedingungen erfüllt und $\rho > n$ (siehe Annahmen) ist $U$ endlich. Die Kapitalakkumulationsgleichung in pro-Kopf Einheiten ist
$$\dot k(t) = y(t) - c(t) - nk(t) = f(k(t)) - c(t) - nk(t)$$wobei $k(t) > 0$ und $f(k(t))$ eine neoklassische Produktionsfunktion ist. Hier könnte man noch eine Abschreibungsquote $\delta$ einbauen, aber das wird der Einfachheit halber weggelassen. Die Kapitalakkumulationsgleichung gibt dem Model die intertemporale Dimension. Das Kapital in der Zukunft hängt von der Konsumentscheidung jetzt ab. Daher ist die Kapitalintensität $k$ als Zustand definiert und der pro-Kopf Konsum $c$ als Steuerung im Sinner der Optimale Steuerung.
Lösung mit Hamilton-Funktion
Wir stellen zunächst die Hamilton-Funktion auf
$$H = u(c(t))e^{nt}+\lambda(t)\big(f(k(t)) - c(t) - nk(t)\big)\;.$$Die FOCs geben sich wie folgt:
- Der Haushalt trifft in jeder Periode die optimale Konsumentscheidung:$$\frac{\partial H}{\partial c(t)} = 0 \implies u'(c(t))e^{nt}-\lambda(t) = 0\;,$$
- Der Haushalt lässt in jeder Periode den optimalen Betrag an Kapital für die Zukunft. $$\dot \lambda(t) = -\frac{\partial H}{\partial k(t)} + \rho\lambda(t) \implies \dot\lambda(t) = -\lambda(t)\left(f'(t) -n\right)+ \rho\lambda(t)$$
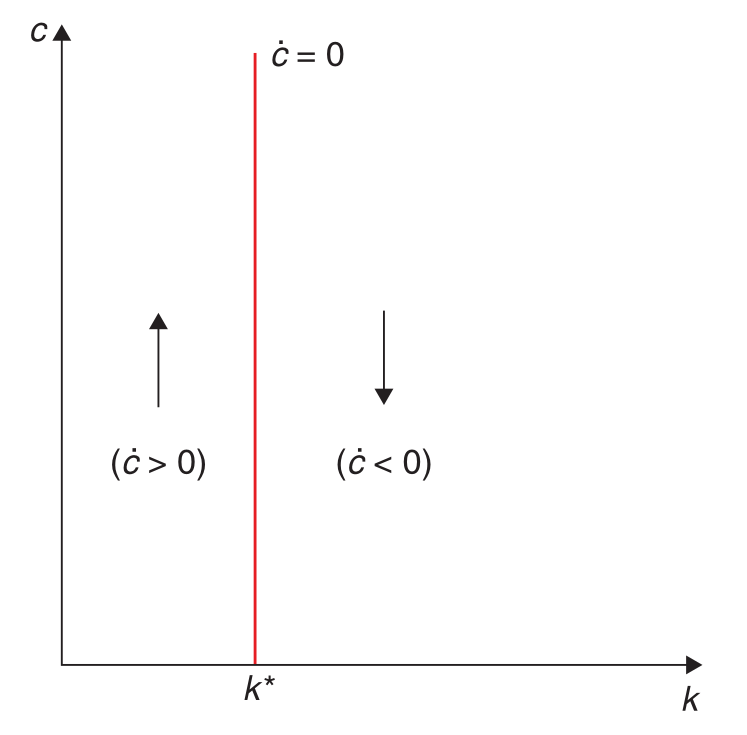
- Die als transversality condition bekannte Bedingung stellt sicher, dass “am Ende” der Haushalt kein Kapital übrig hat. Also alles “verkonsumiert” hat.$$\lim_{t\to\infty} k(t)\lambda(t)e^{-\rho t} = 0\;.$$ Um die Euler-Gleichung zu erhalten leiten wir zuerst die erste FOC nach $t$ ab und erhalten$$ \dot c(t)u''(c(t))e^{nt}+ nu'(c(t))e^{nt} = \dot\lambda(t)\;.$$In den folgenden Schritten teilen wir das Ergebnis durch die erste FOC, Vereinfachen unter anderem mit der $\sigma$, was die intertemporale Elastizität des Konsums ist, und fügen dann die zweite FOC ein: $$\begin{align} &\dot c(t)u''(c(t))e^{nt}+ nu'(c(t))e^{nt} = \dot\lambda(t) &\Huge|\normalsize\text{Siehe Oben}\\\iff&\frac{\dot c(t)u''(c(t))e^{nt}+ nu'(c(t))e^{nt}}{u'(c(t))e^{nt}} = \frac{\dot\lambda(t)}{\lambda(t)}&\Huge|\normalsize\text{$\div$ erste FOC}\\\iff&\frac{\dot c(t)u''(c(t))e^{nt}}{u'(c(t))e^{nt}}+ \frac{nu'(c(t))e^{nt}}{u'(c(t))e^{nt}} = \frac{\dot\lambda(t)}{\lambda(t)}&\Huge|\normalsize\text{Bruchrechnen}\\\iff&\frac{\dot c(t)u''(c(t))}{u'(c(t))}+ n = \frac{\dot\lambda(t)}{\lambda(t)}&\Huge|\normalsize\text{Vereinfachen}\\\iff&\frac{u''(c(t)\dot c(t))}{u'(c(t))} = \frac{\dot\lambda(t)}{\lambda(t)} -n&\Huge|\normalsize\text{Umstellen}\\\iff&\frac{u''(c(t))\dot c(t)c(t)}{u'(c(t))c(t)} = \frac{\dot\lambda(t)}{\lambda(t)} -n&\Huge|\normalsize\text{Erweitern}\\\iff&\frac{\dot c(t)}{c(t)} = \frac{u'(c(t))}{u''(c(t))c(t)}\left(\frac{\dot\lambda(t)}{\lambda(t)} -n\right)&\Huge|\normalsize\text{$\div\frac{u'(c(t))}{u''(c(t))c(t)}$}\\\iff&\frac{\dot c(t)}{c(t)} = -\sigma\left(\frac{\dot\lambda(t)}{\lambda(t)} -n\right)&\Huge|\normalsize\text{Def. $\sigma \equiv-\frac{u'(c(t))}{u''(c(t))c(t)}$}\\\iff&\frac{\dot c(t)}{c(t)} = -\sigma\left(\frac{-\lambda(t)\left(f'(t) -n\right)+ \rho\lambda(t)}{\lambda(t)} -n\right)&\Huge|\normalsize\text{zweite FOC für $\dot\lambda(t)$}\\\iff&\frac{\dot c(t)}{c(t)} = -\sigma(-f'(t) +n + \rho -n)&\Huge|\normalsize\text{Vereinfachen}\\\iff&\frac{\dot c(t)}{c(t)} = \sigma(f'(t) -\rho)&\Huge|\normalsize\text{Vereinfachen}\\\end{align}$$ Letzere Gleichung ist die Euler-Gleichung. Sie beschreibt wie die intertemporale Abwägung des Konsums den Gesamtnutzen maximiert.
Balanced Growth Path (BGP)
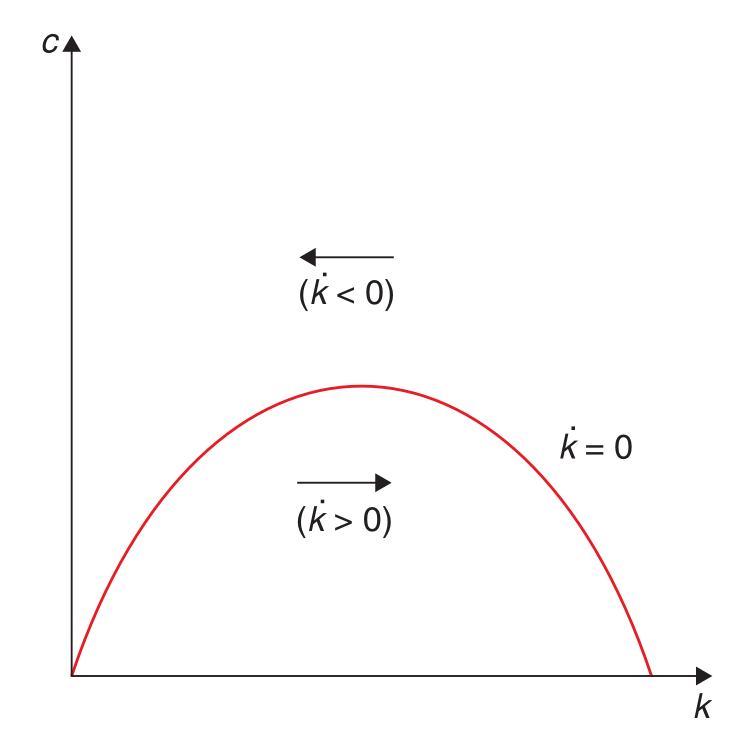
Der BGP ergibt sich wenn mann die Kapitalakkumulationsgleichung gleich Null setzt. So erhält man
$$c^*(t) = f(k^*(t)) - nk^*(t)\;.$$ Der die optimale Konsumfunktion $c^*(t)$ hat also invertiere Parallelform. Gegeben eine Kapitalintensität $k$. Wenn der Konsum höher als das BGP-Niveau ist, dann sinkt $k$. (Und anders herum)
Dezentrale Lösung
Haushalte und Firmen entscheiden selbstständig über Sparquote in einem perfekt kompetitven Markt.