Zwei-Perioden-Modell
Einfache Sprache
Das Zwei-Perioden-Modell besteht aus zwei aufeinander Folgenden Konsum-Sparen-Entscheidungen eines Haushalts. Es muss also herausgefunden werden wie viel der Haushalt in der ersten Periode spart oder leiht für die zweite Periode.
Variablen
| Symbol | Bedeutung | Gegeben |
|---|---|---|
| $t_0$ | aktuelle Zeitperiode (Gegenwart) | Exo. |
| $t_1$ | zukünftige Zeitperiode (Zukunft) | Exo. |
| $r(x)$ | Zinssatz zum Zeitperiode $x$ | Exo. |
| $Y(x)$ | Einkommen in der Zeitperiode $x$ | Exo. |
| $C(x)$ | Konsum in Zeitperiode $x$ | End. |
| $S(x)$ | Gespartes in Zeitperiode $x$ | End. |
| $U$ | Gesamtnutzen | End. |
| $u(\cdot)$ | Nutzenfunktion | Exo. |
| $\beta$ | “Nutzendiskontierwert” | Exo. |
Annahmen
- Ein gibt repräsentativer Haushalt.
- Es gibt kein Geld und Werte sind Realwerte
- Der Haushalt hat ein Einkommen in der Gegenwart und der Zukunft.
- Der Haushalt hat kein Vermögen.
- Der Haushalt kann sparen oder leihen zum Zinssatz $r$.
- Der Haushalt muss zu jedem Zeitpunkt $t$ entscheiden wie viel er spart und investiert.
- Die Nutzenfunktion $u(\cdot)$ hat folgende Eigenschaften:
- Der Grenznutzen ist positiv $u'(\cdot)>0$ (siehe Grenzprodukt). Also “Mehr ist Besser”.
- Der Grenznutzen ist abnehmend $u''(\cdot)<0$ (siehe Grenzprodukt). Je weiter der Konsum steigt desto geringer wächst der Nutzen.
Aufbau
Budget-Bedingung
Da der Haushalt in zwei Zeitperioden lebt gibt es für beide ein Bedingung für das Budget:
$$\begin{align}C(t_0)+S(t_0) &\leq Y(t_0)\\C(t_1)+S(t_1) &\leq Y(t_1)+(1+r(t_0))S(t_0)\end{align}$$Beachte, dass das Gesparte $S(x)$ positiv, Null oder negativ (durch Leihen) sein kann. Zweite kann aus wie folgt geschrieben werden
$$C(t_1)+S(t_1) - S(t_0)\leq Y(t_1)+r(t_0)S(t_0)\;.$$Wir setzten zusätzlich voraus das
- $S(t_1) = 0$. Dies ist under der Endbedingung bekannt. Intuitiv würde $S(t_1) >0$ bedeuten das der Haushalt Erspartes in eine Periode mitnimmt in der er nicht mehr existiert. Genau so soll auch nicht erlaubt sein mit Schulden zu sterben.
- Unter den konventionellen Annahmen über Präferenzen wird ein Haushalt all ihm zu Verfügung stehenden Resourcen verwenden. Daher Ändern sich die Bedingungen wie folgt $$\begin{align}C(t_0)+S(t_0) &= Y(t_0)\\C(t_1) &=Y(t_1)+(1+r(t_0))S(t_0)\end{align}$$ In dem wir die Gleichungen nach $S(t_0)$ umstellen und gleich setzen erhalten wir die intertemporale Budget-Bedingung $$C(t_0)+\frac{C(t_1)}{1+r(t_0)}=Y(t_0)+\frac{Y(t_1)}{1+r(t_0)}\;.$$ Die Gleichung besagt das Konsum und Einkommen gleich seine müssen im Gegenwarts-Kontext. Dazu wird z.B. das zukünftige Einkommen mit der Zinsrate diskontiert.
Zielfunktion
Wir nehmen an das der Gesamtnutzen $U$ die Summe der Nutzen von den zwei Perioden ist. Dabei wird der Nutzen in der zukünftigen Periode um $\beta$, mit $0\leq\beta<1$, diskontiert. Das heißt der Haushalt zieht aktuellen Konsum zukünftigen Konsum vor. Also
$$U = u(C(t_0))+\beta u(C(t_1))\;.$$Bemerke das $\beta$ der “Nutzendiskontierwert” ist und $\frac{1}{1+r(t)}$ der “Güterdiskontierwert ist”.
Lösung
Wir formulieren zunächst das Optimierungsproblem wie folgt:
Problemstellung:
Es soll
$$\max_{C(t_0),C(t_1)} U=u(C(t_0))+\beta u(C(t_1))$$unter der Bedingung, dass
$$C(t_0)+\frac{C(t_1)}{1+r(t_0)}=Y(t_0)+\frac{Y(t_1)}{1+r(t_0)}\;.$$
Wir stellen zunächst die Bedingung nach $C(t_1)$ um so, dass
$$C(t_1) = (1+r(t_0))(Y(t_0)-C(t_0))+Y(t_1)\;.$$Das erlaubt uns die das Problem vereinfachen zu
$$\max_{C(t_0)} U=u(C(t_0))+\beta u((1+r(t_0))(Y(t_0)-C(t_0))+Y(t_1))\;. $$Das Problem ist jetzt nur noch ein einfaches Maximierungsproblem. Für dessen Lösung müssen wir die FOC gleich Null setzen. Also
$$\frac{\partial U}{\partial C(t_0)}= u'(C(t_0))+\beta u'((1+r(t_0))(Y(t_0)-C(t_0))+Y(t_1))\cdot-(1+r(t_0)) = 0\;.$$Das lässt sich vereinfachen zu
$$u'(C(t_0)) = \beta(1+r(t_0))u'(C(t_1))\;.$$Dies ist die Euler-Gleichung des Konsums. Im Optimum muss also $C(t_0)$ und $C(t_1)$ so gewählt werden, dass der Grenznutzen in $t$ gleich dem Grenznutzen in $t_1$, diskontiert mit $\beta$ , weil Gegenwart mehr wert ist als Zukunft, und multipliziert mit $1+r(t_0)$, was den zuwachs durchs sparen darstellt. Umgestellt ergibt sich
$$\frac{u'(C(t_0))}{\beta u'(C(t_1))} = 1+r(t_0)\;.$$Graphische Analyse
Wir nutzen eine Graphik mit Budgetlinie und Indifferenzkurve. Die Graphik hat als $x$- bzw. $y$-Achse $C(t_0)$ bzw. $C(t_1)$. Als Budgetlinie nehmen wir die Bedingung des Budget, leicht umgestellt damit die Abhängigkeit von $C(t_1)$ von $C(t_0)$ deutlich wird,
$$C(t_1) = -(1+r(t_0))C(t_0)+(1+r(t_0))Y(t_0)+Y(t_1)\;.$$ Graphisch also 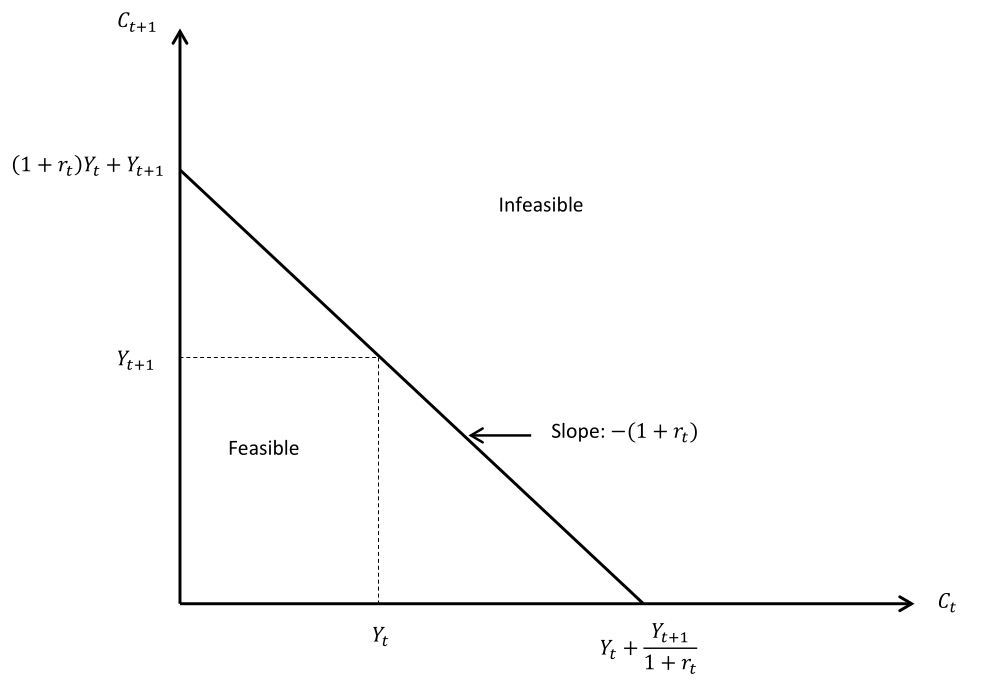 Dazu kommt die Indifferenzkurven bezüglich des Gesamtnutzen $U$. Es gibt verschiedene Indifferenzkurven für verschiedene Gesamtnutzen-Größen. Angenommen ein Haushalt hat das Konsumbündel $(C_0(t_0),C_0(t_1))$.
Der Gesamtnutzen $U_0$ ist gegeben durch $U_0=u(C_0(t_0))+\beta u(C_0(t_1))$. Eine Veränderung $dU$ von $U$ kann sich daher nur aus Veränderungen in $C(t_0)$ und $C(t_1)$ ergeben, respektiv $dC(t_0)$ und $dC(t_1)$. Es ergibt sich durch Ableitung
Dazu kommt die Indifferenzkurven bezüglich des Gesamtnutzen $U$. Es gibt verschiedene Indifferenzkurven für verschiedene Gesamtnutzen-Größen. Angenommen ein Haushalt hat das Konsumbündel $(C_0(t_0),C_0(t_1))$.
Der Gesamtnutzen $U_0$ ist gegeben durch $U_0=u(C_0(t_0))+\beta u(C_0(t_1))$. Eine Veränderung $dU$ von $U$ kann sich daher nur aus Veränderungen in $C(t_0)$ und $C(t_1)$ ergeben, respektiv $dC(t_0)$ und $dC(t_1)$. Es ergibt sich durch Ableitung
Da auf der Indifferenzkurve die Änderung des Nutzen gleich Null sein muss, können wir $dU = 0$ setzen. Nach umstellen ergibt sich
$$\frac{dC(t_1)}{dC(t_0)}= -\frac{u'(C_0(t_0))}{\beta u'(C_0(t_1))}\;.$$ Das sagt uns, dass die Steigung der Indifferenzkurve mit $U= U_0$ an der Stelle $(C_0(t_0),C_0(t_1))$ das negierte Verhältnis zwischen den Grenznutzen ist. Die Negativität ergibt intuitiv Sinn, da eine Erhöhung des Konsums in $t_0$ zwangsläufig eine Verminderung des Konsums in $t_1$ mit sich zieht, wenn der Gesamtnutzen gleich bleiben soll. Da wir von abnehmendem Grenznutzen ausgehen, ist die Indifferenzkurve Konvex geformt. Es ergibt sich folgendes Bild 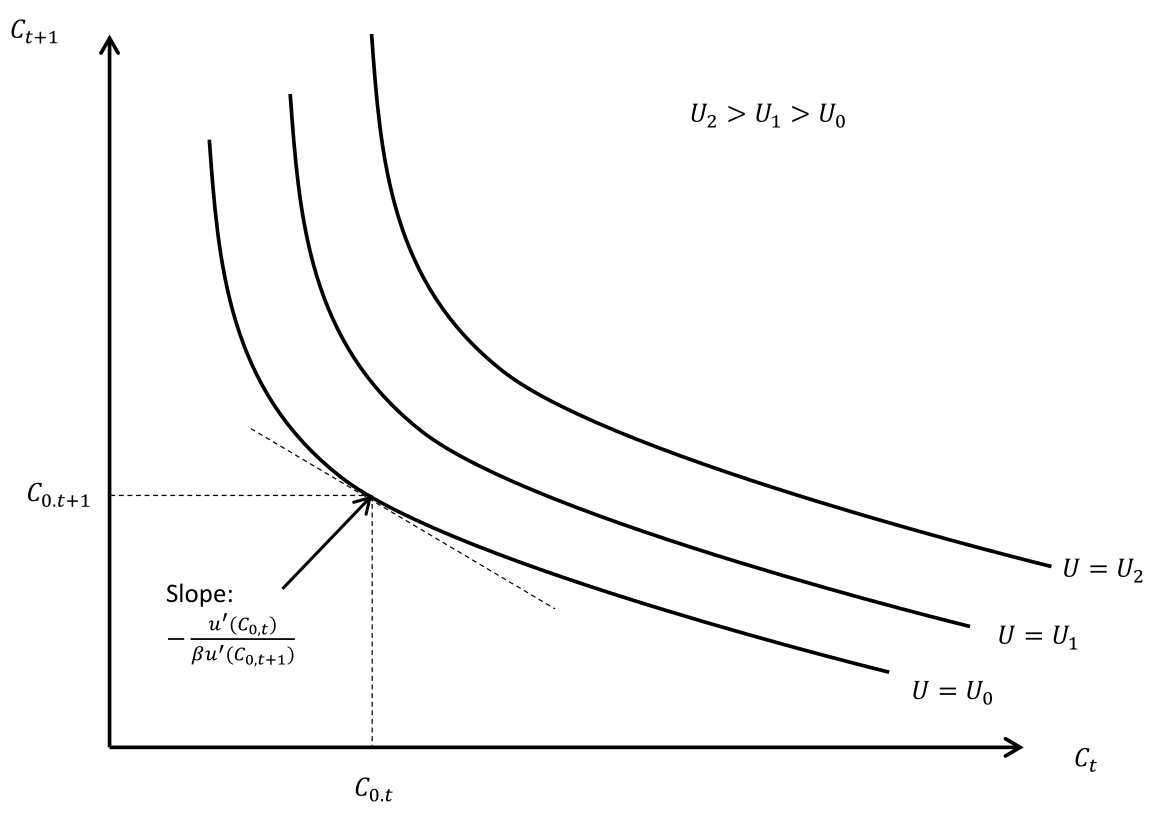 Das Optimierungsproblem kann Graphisch so verstanden werden, dass die höchst Mögliche Indifferenzkurve gewählt werden soll, ohne die Budgetlinie zu überschreiten. Also folgende Situation
Das Optimierungsproblem kann Graphisch so verstanden werden, dass die höchst Mögliche Indifferenzkurve gewählt werden soll, ohne die Budgetlinie zu überschreiten. Also folgende Situation 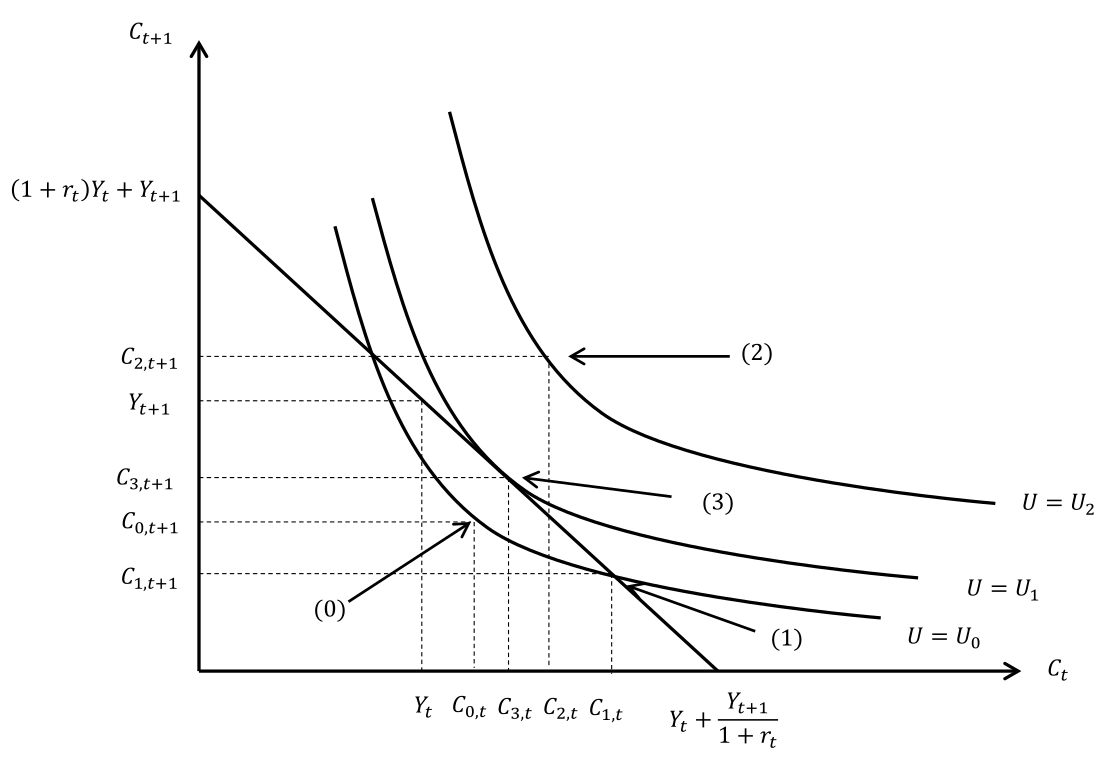 in der nur das Konsumbündel $(C_3(t_0),C_3(t_1))$ optimal ist.
in der nur das Konsumbündel $(C_3(t_0),C_3(t_1))$ optimal ist.
Mit dieser graphischen Darstellung lassen sich Veränderung Analysieren. Hier werden nur Erhöhungen betrachtet. Verringerungen haben ähnliche Effekte nur umgekehrte Richtung.
Erhöhung des jetzigen Einkommens
In diesem Beispiel ist die Ausgangssituation mit $_0$ und nach der Veränderung mit $_1$ beschriftet. Wir nehmen an das $C_0(t_0)>Y_0(t_0)$. Also das in $t_0$ geliehen wird. Mit einer Erhöhung von $Y(t_0)$ (alles andere bleibt gleich) schiebt sich nun die Budgetlinie nach Oben ohne die Steigung zu ändern.
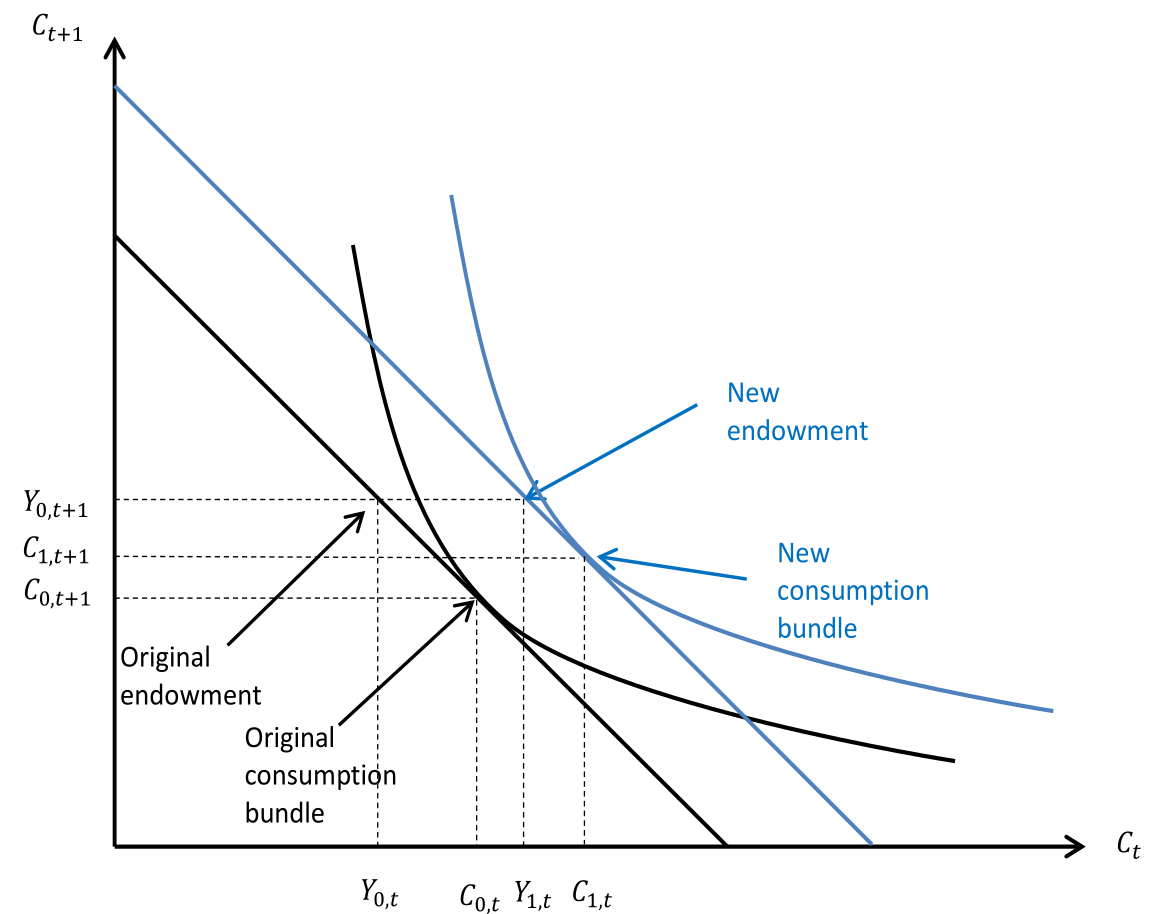 Wir sehen das $C(t_0)$ steigt wenn $Y(t_0)$ steigt. Aber da auch $C(t_1)$ mit steigt ist, steigt $C(t_0)$ weniger als $Y(t_0)$. Wir sehen auch das sich das Gesparte in $t_0$ erhöht haben muss.
Wir sehen das $C(t_0)$ steigt wenn $Y(t_0)$ steigt. Aber da auch $C(t_1)$ mit steigt ist, steigt $C(t_0)$ weniger als $Y(t_0)$. Wir sehen auch das sich das Gesparte in $t_0$ erhöht haben muss.
Erhöhung des zukünftigen Einkommens
In diesem Beispiel ist die Ausgangssituation mit $_0$ und nach der Veränderung mit $_1$ beschriftet. Mit einer Erhöhung von $Y(t_1)$ (alles andere bleibt gleich) schiebt sich nun die Budgetlinie wieder nach Oben ohne die Steigung zu ändern.
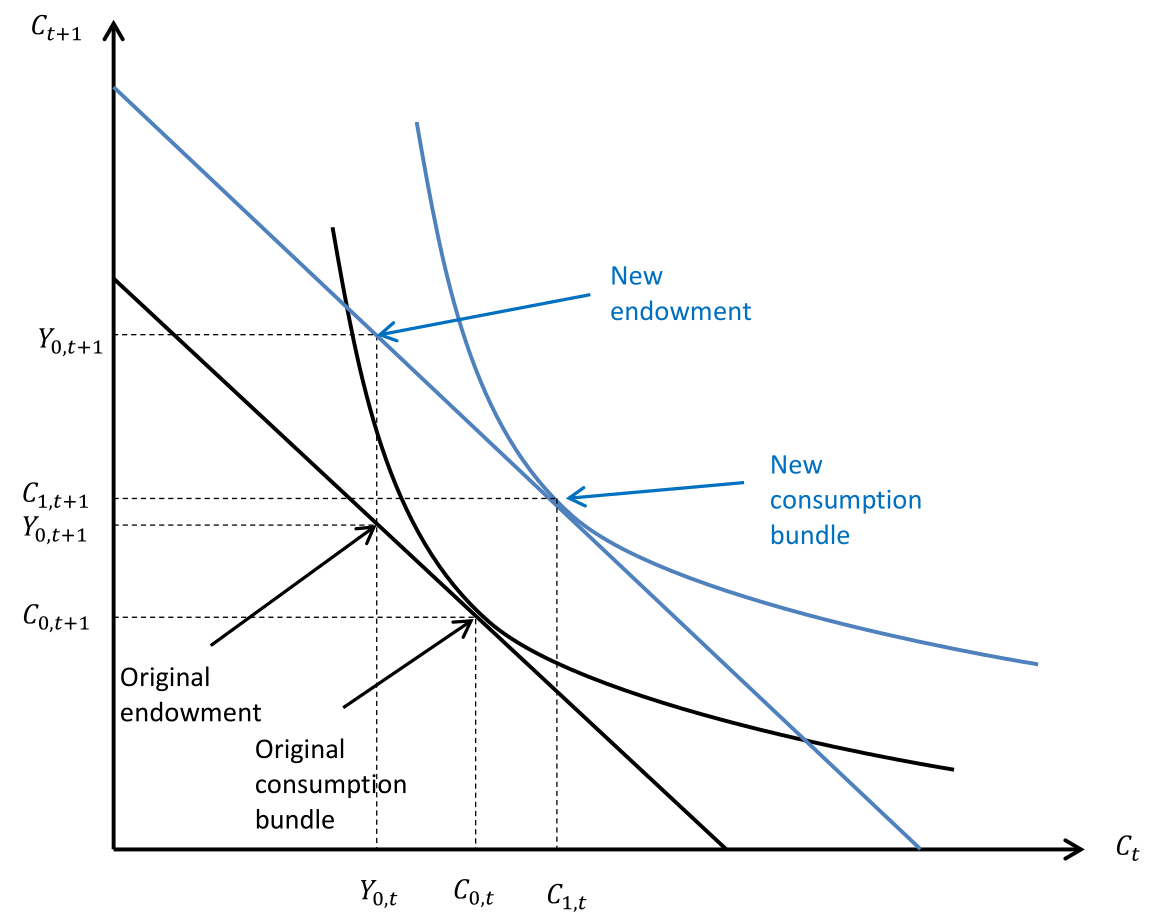 Wir sehen das wieder das der Konsum in beiden Perioden steigt. Das heißt es wird mehr geliehen in der ersten Periode, da sich auf ein höheres Einkommen später verlassen wird.
Wir sehen das wieder das der Konsum in beiden Perioden steigt. Das heißt es wird mehr geliehen in der ersten Periode, da sich auf ein höheres Einkommen später verlassen wird.
Konsum glätten
Wir sehen das Konsum in alle Perioden erhöht werden soll. Also den Konsum glätten. Das ist die Konsequenz der Annahmen abnehmendem Grenznutzen,
Erhöhen der Zinsrate
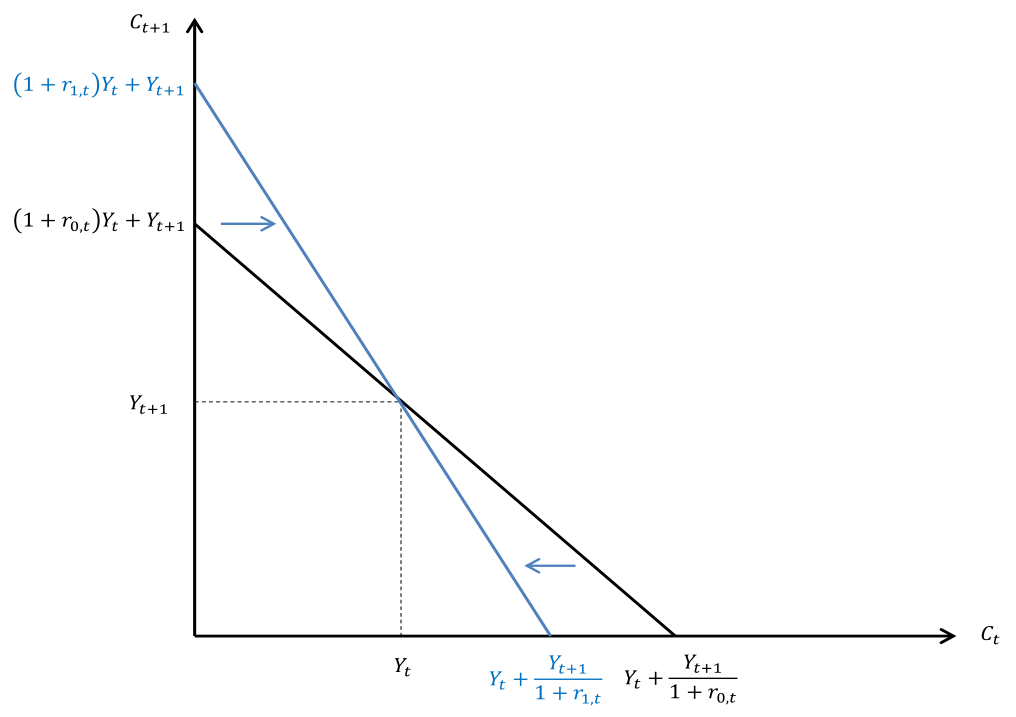
Zunächst dreht sich die Budgetlinie um den Punkt $(Y(t_0),Y(t_1))$, da die Einkommen nicht verändert werden.
Der mögliche Konsum in der zweite Periode erhöht sich da sich Sparen mehr lohnt. Dem entgegengesetzt sinkt der mögliche Konsum in der ersten Periode da leihen teurer wird.
Borger in erster Periode
Wir nehmen an das in der ersten Periode geliehen wird. Also $C(t_0)> Y(t_0)$.
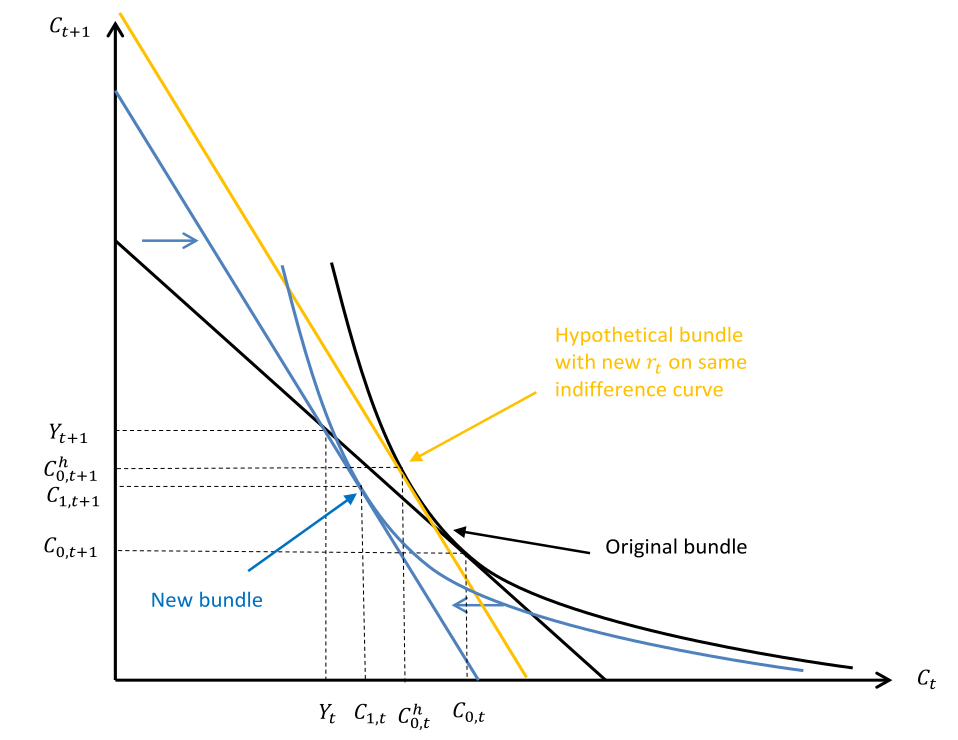 In Blau ist neue Budgetlinie. Die hypothetische Budgetlinie ergibt wenn die neue Steigung der Budgetlinie an die alte Indifferenzkurve gehalten wird. Die Bewegung von dem alten Konsumbündel zu dem Bündel $(C^h(t_0),C^h(t_1))$, gegeben durch der hypothetische Budgetlinie, nennt man Substitutionseffekt. Es spiegelt den Konsum wieder wenn der Haushalt so viel Entschädigung bekommt um sein Nutzenniveau zu halten.
In Blau ist neue Budgetlinie. Die hypothetische Budgetlinie ergibt wenn die neue Steigung der Budgetlinie an die alte Indifferenzkurve gehalten wird. Die Bewegung von dem alten Konsumbündel zu dem Bündel $(C^h(t_0),C^h(t_1))$, gegeben durch der hypothetische Budgetlinie, nennt man Substitutionseffekt. Es spiegelt den Konsum wieder wenn der Haushalt so viel Entschädigung bekommt um sein Nutzenniveau zu halten.
Sparer in erster Periode
Wir nehmen an das in der ersten Periode gespart wird. Also $C(t_0)< Y(t_0)$.
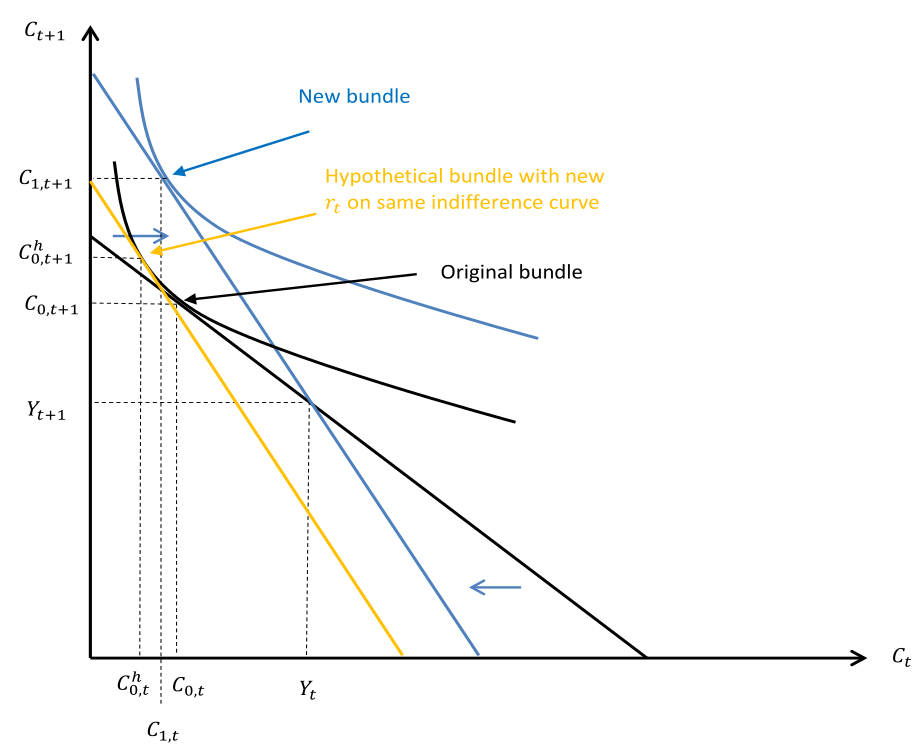
Anwendungen
Zusammenfassung
- Konsum hängt vom aktuellen und zukünftigen Einkommen ab.
- Wenn der Haushalt zusätzliches Einkommen in der Gegenwart oder Zukunft antizipiert, dann wird er den Konsum sowohl in der Gegenwart als auch in der Zukunft erhöhen. Der Haushalt will also den Konsum glätten.
- Der Effekt einer Zinssatzänderung auf den Konsum hängt von zwei Faktoren ab: Der Substitutionseffekt sorgt dafür das weniger konsumiert wird um mehr zu sparen. Der Einkommenseffekt ist dem entgegengesetzt.