Solow-Modell
Einfache Sprache
Das Solow-Modell erklärt das Wachstum nur vom Bevölkerungswachstum und der technologische Entwicklung abhängt. So gibt es auf langer Sicht ein Gleichgewicht zwischen Investition und Abschreibung. Haupterkenntnis ist, dass das eingesetzte Kapital pro-Kopf (Kapitalintensität) konstant bleibt und daher auch das pro-Kopf Einkommen.
Unten Beschrieben ist das klassische Solow-Modell in seiner einfachsten Form. Folgende Modelle sind “erweiterte” Solow-Modelle
Einfaches Solow-Modell
Variablen
| Symbol | Bedeutung | Formel |
|---|---|---|
| $K$ | Kapital | |
| $L$ | Arbeit | |
| $E_t$ | Humankapital | $L_t\cdot e^{\lambda t}$ |
| $A$ | Technologie | |
| $Y$ | Output | |
| $H$ | Humankapital | |
| $s$ | Sparquote | |
| $\delta$ | Abschreibungsquote | |
| $C$ | Konsum | |
| $I$ | Investition | |
| $T$ | Technologie | |
| $k$ | Kapitalintensität | $K/L$ |
| $y$ | Produktionsertrag pro Arbeitseinheit | $Y/L$ |
| $\gamma_k$ | Wachstumsrate der Kapitalintensität | |
| $k^*$ | Variablen auf einem BGP z.B. Kapitalintensität $k$ | |
| $k_g$ | Optimaler Kapitalintensität pro Kopf nach der Golden Rule | |
| $c_g$ | Optimaler Konsum pro Kopf nach der Golden Rule | |
| $n$ | Bevölkerungswachstum | |
| $s_k$ | Sparquote für Kapital | |
| $s_h$ | Sparquote für Humankapital |
- Variablen mit einem Punkt drüber sind die Differenzen bezüglich der Zeit, z.B. $\dot K = K/t$.
- Kleinbuchstabige Variablen sind sind die Differenzen bezüglich der Einwohner, z.B. $k = K/L$ aber auch $f = F/L$ (also die Pro-Kopf-Produktionsfunktion).
Annahmen
- Die Volkswirtschaft wird in einem einzigen Haushalt zusammengefasst.
- Die Produktionsfunktion $F$ ist eine neoklassische Produktionsfunktion mit $Y = F(K,L)$.
- Die gesamte Population arbeitet und wächst mit einer konstanten positiven Rate $n$ definiert durch $\dot L/L =n\geq 0$.
Aufbau
Die zeitliche Veränderung von $K$ setzt sich aus dem gesparten Teil des Produktionsergebnisses und der Abnutzung des bestehenden Kapitals zusammen. D.h.
$$\dot K = I - \delta K = sF(K,L) - \delta K\;.$$ist. Die Änderungsrate der Kapitalintensität $\dot k$ ist gegeben durch die Fundamentale Bewegungsgleichung des Solow-Modells. Die optimale Kapitalintensität $k^*$ wird im BGP erreicht, zu dem jede Ökonomie über die Zeit konvergiert.Unter allen Möglichen BGPs, welche sich aus unterschiedlichen Sparquoten ergeben, maximiert eine Sparquote den Konsum. Diese optimale Sparquote wird mit der Golden Rule ermittelt und resultiert in der maximalen Konsum pro Kopf $c_g$. Hat eine Ökonomie eine Sparquote $s$ ungleich der optimalen Sparquote $s_g$, dann könnte es jedem Besser gehen, wenn $s$ sich $s_g$ annähert. Die Differenz im pro-Kopf Konsum nennt man dynamic inefficiency.
Anwendung
Konvergenz
Um Konvergenz zu zeigen leiten wir erst die Formel für die Änderungsrate der Kapitalintensität her. Das ist die Fundamentale Bewegungsgleichung geteilt durch $k$.Also
$$\gamma_k = \frac{\dot k}{k} = \frac{sf(k)}{k}-(n+\delta)\;.$$Als nächstes leiten wir $\gamma_k$ nach $k$ ab um den Einfluss der Kapitalintensität auf die Änderungsrate der Kapitalintensität zu identifizieren
$$\frac{\partial\gamma_k}{\partial k}= \frac{sf'(k)k - sf(k)}{k^2} = \frac{s}{k}\left(f'(k)-\frac{f(k)}{k}\right)$$Da $f$ abnehmende Grenzerträge hat (wegen neoklassische Produktionsfunktion) ist das Grenzprodukt $f'(k)$ kleiner als das Durchschnittsprodukt $\frac{f(k)}{k}$ gilt
$$\frac{\partial\gamma_k}{\partial k}< 0\;.$$Also wenn $k$ steigt dann sinkt $\gamma_k$ und wenn $k$ sinkt dann steigt $\gamma_k$.
Graphisch sieht das wie folgt aus: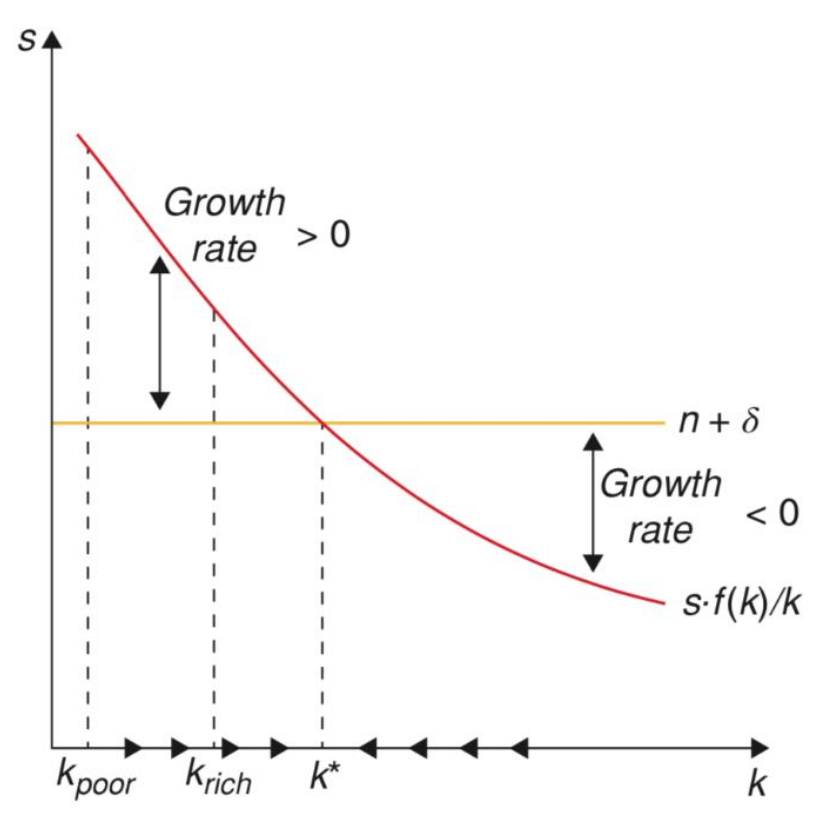 
Hier sehen wir das die Wachstumsrate $\gamma_k$ die Differenz zwischen $sf(k)/k$ und $n+\delta$ ist.
Konditionale Konvergenz
Einfache Sprache
Wenn sich zwei Ökonomien sich nur in der initialen Kapitalintensität $k(0)$ unterscheiden. Also Gleich sind bezüglich $f(\cdot)$,$s$,$n$ und $\delta$. Dann werden beide Ökonomien zu dem gleichen BGP konvergieren. Dabei ist die Wachstumsrate für die Ökonomie mit der niedrigeren Kapitalintensität zu begin größer. Daraus folgt, dass arme Länder reiche Länder einholen können bzgl. Entwicklung gegeben sie sind strukturell ähnlich.
Das Solow-Modell impliziert konditionale Konvergenz.
Absolute Konvergenz
Einfache Sprache
Absolute Konvergenz besagt das arme Ökonomien schneller wachsen als reiche Ökonomien unabhängig von den Charakteristiken der Ökonomien.
Warnung
Das Solow-Modell impliziert nicht absolute Konvergenz.
Einkommensunterschiede
Das Solow-Modell kann nicht die beobachtbaren Einkommensunterschiede durch die Sparquote erklären. Aber unter Annahme von Produktivitäts-Unterschiede stimmen Beobachtungen mit dem Solow-Modell überein.
Herleitung
Der Einkommensunterschied zwischen zwei Ökonomien ist die Differenz zwischen den pro-Kopf Outputs im BGP ${y_1^*}/{y_2^*}$.
Einklang mit Kaldor facts
Hier schauen wir ob das Solow-Modell die Kaldor facts erklären kann.
| Fakt | Beschreibung | Erfüllt | Solow-Model |
|---|---|---|---|
| 1 | Pro-Kopf Output $y$ wächst kontinuierlich. | ✔️ | Wird technologische Entwicklung (Produktivitätszuwachs) angenommen wächst $y$ mit der Rate der technologische Entwicklung (Produktivitätszuwachs). |
| 2 | Kapital-Output-Verhältnis ist konstant. | ✔️ | Da $K = kL$ und $Y = yL$ folgt $K/Y = k/y$. Im BGP (balanced growth path) ist sowohl $k$ als auch $y$ konstant. Somit muss auch $K/Y$ konstant sein. |
| 3 | Kapitalintensität $k$ wächst kontinuierlich. | ❌ | Im BGP (balanced growth path) ist $k$ konstant. |
| 4 | Return on capital $r$ ist konstant. | ✔️ | Mit einer Cobb-Douglas-Funktion ist der Return on capital konstant. |
| 5 | Arbeit und Kapital bekommen konstante Anteile des Outputs | ✔️ | Mit einer Cobb-Douglas-Funktion ergeben sich konstante Anteile. |
| 6 | Die Änderungsrate von $y$ ist in verschiedenen Ökonomien unterschiedlich groß. | ✔️ | Durch Unterschiedliche Änderungsrate der technologische Entwicklung (Produktivitätszuwachs) erklärt. |
Pro-Kopf Output $y$ wächst kontinuierlich.
Wird technologische Entwicklung angenommen wächst $y$ mit der Rate der technologische Entwicklung.
Kapital-Output-Verhältnis ist konstant.
Da $K = kL$ und $Y = yL$ folgt $K/Y = k/y$. Im BGP ist sowohl $k$ als auch $y$ konstant. Somit muss auch $K/Y$ konstant sein.
Kapitalintensität $k$ wächst kontinuierlich.
Im BGP ist $k$ konstant.
Return on capital $r$ ist konstant.
Wir nutzen eine Cobb-Douglas-Funktion mit $Y = AK^\alpha L^{1-\alpha}$. Dann ergibt sich der Lohn $w$ als das Grenzprodukt der Arbeit, also
$$w = (1-\alpha)AK^\alpha L^{-\alpha} = (1-\alpha)Ak^\alpha = \textrm{MPL}\;,$$und der Return on capital $r$ als das Grenzprodukt des Kapitals, also
$$r = \alpha AK^{\alpha-1}L^{1-\alpha} = \alpha AK^{\alpha-1}L^{-(\alpha-1)} = \alpha A\frac{K^{\alpha-1}}{L^{\alpha-1}} = \alpha Ak^{\alpha -1} = \textrm{MPK}\;.$$Wir setzen nun den aus der Cobb-Douglas-Funktion resultierenden BGP $k^* = \left(\frac{sA}{n+\delta}\right)^{\frac{1}{1-\alpha}}$ ein. Wir erhalten
$$w^* = (1-\alpha)A\left(\frac{sA}{n+\delta}\right)^{\frac{\alpha}{1-\alpha}} = (1-\alpha)A^{\frac{1}{1-\alpha}}\left(\frac{s}{n+\delta}\right)^{\frac{\alpha}{1-\alpha}}$$und
$$r^* = \alpha A\left(\frac{sA}{n+\delta}\right)^{\frac{\alpha -1}{1- \alpha}} = \alpha A\left(\frac{sA}{n+\delta}\right)^{-1} = \alpha\frac{n+\delta}{s}\;.$$Wir sehen, das in $r^*$ nur Variablen enthält die im BGP konstant sind.
Arbeit und Kapital bekommen konstante Anteile des Outputs
Wir multiplizieren zunächst Arbeit $L$ mit dem Lohn $w$, um den Teil Outputs zu bekommen dem der Arbeit zusteht. Das Produkt teilen wir dann durch den Gesamtoutput $Y$.
$$\begin{align} \frac{wL}{Y} &= \frac{(1-\alpha)AK^\alpha L^{-\alpha}L}{AK^\alpha L^{1-\alpha}}&\Huge|\normalsize\text{Def. $w$, Def. $Y$}\\ &= 1-\alpha&\Huge|\normalsize\text{Vereinfachen}\end{align}$$Analog verfahren wir für Kapital $K$ und [Return on capital $r$.
$$\begin{align} \frac{rK}{Y} &= \frac{\alpha AK^{\alpha-1} L^{1-\alpha}K}{AK^\alpha L^{1-\alpha}}&\Huge|\normalsize\text{Def. $w$, Def. $Y$}\\ &=\alpha&\Huge|\normalsize\text{Vereinfachen}\end{align}$$Es ist nun ersichtlich das sowohl $\frac{wL}{Y}$ als auch $\frac{rK}{Y}$ konstant sind.
Die Änderungsrate von $y$ ist in verschiedenen Ökonomien unterschiedlich groß.
Durch Unterschiedliche Änderungsrate der technologische Entwicklung erklärt. Die technologische Entwicklung selbst wird nicht erklärt!
Zusammenfassung und Vorhersagen des Models
- Langfristig (BGP) ist technologische Entwicklung die einzige Quelle pro Kopf Einkommenswachstum.
- Anhaltende Unterschiede zwischen Ökonomien lassen sich daher durch Produktivitäts-Unterschiede erklären.
- Es kann sein das die Sparquote nicht optimal gewählt ist.
- Das Model erklärt aber nicht die technologische Entwicklung.
- Auch die Sparquote exogen gewählt und daher unter Umständen nicht optimal.